
【题目】已如长方形![]() 中,
中,![]() ,M为
,M为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,
,
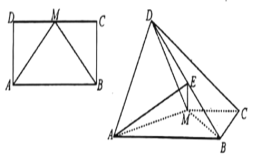
(1)求证:![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的中点,求三棱锥
上的中点,求三棱锥![]() 与四棱锥
与四棱锥![]() 的体积的比值 .
的体积的比值 .
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】一种作图工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆
的中点,短杆![]() 可绕
可绕![]() 转动,长杆
转动,长杆![]() 通过
通过![]() 处铰链与
处铰链与![]() 连接,
连接,![]() 上的栓子
上的栓子![]() 可沿滑槽AB滑动,且
可沿滑槽AB滑动,且![]() ,
,![]() .当栓子
.当栓子![]() 在滑槽AB内作往复运动时,带动
在滑槽AB内作往复运动时,带动![]() 绕
绕![]() 转动一周(
转动一周(![]() 不动时,
不动时,![]() 也不动),
也不动),![]() 处的笔尖画出的曲线记为
处的笔尖画出的曲线记为![]() .以
.以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
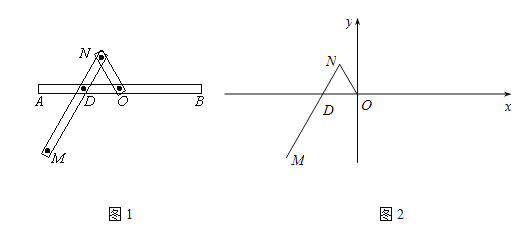
(Ⅰ)求曲线C的方程;
(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线
总与曲线![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,数列
是公差为正数的等差数列,数列![]() 为等比数列,且
为等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 是由所有
是由所有![]() 的项,且
的项,且![]() 的项组成的数列,且原项数先后顺序保持不变,求数列
的项组成的数列,且原项数先后顺序保持不变,求数列![]() 的前2019项的和
的前2019项的和![]() ;
;
(3)对任意给定的![]() 是否存在
是否存在![]() 使
使![]() 成等差数列?若存在,用
成等差数列?若存在,用![]() 分别表示
分别表示![]() 和
和![]() (只要写出一组即可);若不存在,请说明理由.
(只要写出一组即可);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线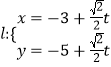 (
(![]() 为参数)与曲线
为参数)与曲线![]() 相交于点
相交于点![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856331)
甲、乙两家快餐店对某日7个时段的光顾的客人人数进行统计并绘制茎叶图如下图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
(Ⅰ)求a,b的值,并计算乙数据的方差;
(Ⅱ)现从乙数据中不大于16的数据中随机抽取两个,求至少有一个数据小于10的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的方程为(x-1)2+(y-1)2=9,P(2,2)是该圆内一点,过点P的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是______ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值.由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4∶2∶1.
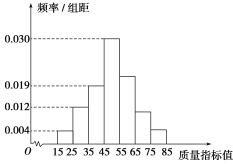
(1)求这些产品质量指标值落在区间[75,85]内的概率;
(2)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间[45,75)内的产品件数为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第![]() 代“勾股树”所有正方形的个数与面积的和分别为( )
代“勾股树”所有正方形的个数与面积的和分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若满足
,若满足![]() ,则称函数
,则称函数![]() 为“
为“![]() 型函数”.
型函数”.
(1)判断函数![]() 和
和![]() 是否为“
是否为“![]() 型函数”,并说明理由;
型函数”,并说明理由;
(2)设函数![]() ,记
,记![]() 为函数
为函数![]() 的导函数.
的导函数.
①若函数![]() 的最小值为1,求
的最小值为1,求![]() 的值;
的值;
②若函数![]() 为“
为“![]() 型函数”,求
型函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com