如图，四棱柱
中，底面ABCD是矩形，且
，
，
，若O为AD的中点，且
．
（1）求证：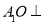
平面ABCD；
（2）线段BC上是否存在一点P，使得二面角
为
？若存在，求出BP的长；不存在，说明理由．
轻松课堂单元期中期末专题冲刺100分系列答案科目：高中数学 来源：2015-2016学年江西省吉安市高二上期中文科数学试卷（解析版） 题型：解答题
（本小题满分12分）如图，
内接于圆O，AB是圆O的直径，
，
，
，四边形DCBE为平行四边形，
平面ABC.
（1）证明：平面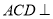
平面ADE；
（2）在CD上是否存在一点M，使得
平面ADE？证明你的结论.
查看答案和解析>>
科目：高中数学 来源：2015-2016学年江西省吉安市高二上期中理科数学试卷（解析版） 题型：选择题
已知实数a，b，则“
”是“
”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要
查看答案和解析>>
科目：高中数学 来源：2015-2016学年安徽省合肥市高一上学期期中数学试卷（解析版） 题型：解答题
已知函数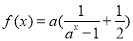
，其中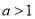
．
（1）判断并证明函数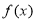
的奇偶性；
（2）判断并证明函数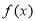
的单调性．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年广东省普宁市华美实验学校高一上学期期中数学试卷（解析版） 题型：填空题
设23－2x＜0．53x－4，则x的取值范围是________．
查看答案和解析>>
科目：高中数学 来源：2016届山西省高三10月月考理科数学试卷（解析版） 题型：解答题
甲箱子里装有3个白球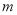
个黑球，乙箱子里装有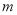个白球，2个黑球，在一次试验中，分别从这两个箱子里摸出一个球，若它们都是白球，则获奖
（1） 当获奖概率最大时，求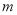的值；
（2）在（1）的条件下，班长用上述摸奖方法决定参加游戏的人数，班长有4次摸奖机会（有放回摸取），当班长中奖时已试验次数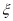
即为参加游戏人数，如4次均未中奖，则
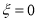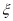，求的分布列和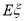
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图像如图所示，则
．
是虚数单位，复数
，则
=（ ）
C．
D．2
内是增函数的为（ ）
，
，
，且
，
，