
【题目】已知函数![]() ,
,![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调区间;
的单调区间;
(3)若函数![]() 在定义域内恒有
在定义域内恒有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;
(3)![]() .
.
【解析】【试题分析】(1)借助导数的几何意义建立方程组求解;(2)先求导再借助导数与函数单调性之间的关系求解;(3)先将不等式进行等价转化,再分离参数借助导数知识求其最值,即可得到参数的范围。
(1)由题意,得![]() ,
,
则![]() ,∵在点
,∵在点![]() 处的切线方程为
处的切线方程为![]() ,
,
∴切线斜率为![]() ,则
,则![]() ,得
,得![]() ,
,
将![]() 代入方程
代入方程![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴![]() ,将
,将![]() 代入得
代入得![]() ,
,
故![]() .
.
(2)依题意知函数的定义域是![]() ,且
,且![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
故![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(3)由![]() ,得
,得![]() ,
,
∴![]() 在定义域
在定义域![]() 内恒成立.
内恒成立.
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() .
.
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
故![]() 在定义域内有极小值
在定义域内有极小值![]() ,此极小值又为最小值.
,此极小值又为最小值.
∴![]() 的最小值为
的最小值为![]() ,
,
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 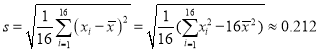 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,直线
,直线![]() :
: ![]() 与以原点为圆心、椭圆
与以原点为圆心、椭圆![]() 的短半轴长为半径的圆
的短半轴长为半径的圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,与圆
,与圆![]() 相交于两点
相交于两点![]() ,
, ![]() ,若
,若![]() 是钝角三角形,求直线
是钝角三角形,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
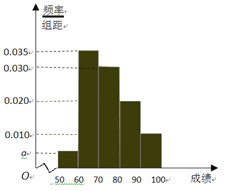
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线![]() 的参数方程为
的参数方程为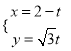 (t为参数),P、Q分别为直线
(t为参数),P、Q分别为直线![]() 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数图象恰好经过k个格点,则称函数为k阶格点函数.已知函数:
①y=sinx; ②y=cos(x+![]() ); ③y=ex-1; ④y=x2.
); ③y=ex-1; ④y=x2.
其中为一阶格点函数的序号为 ( )
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com