
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | … |
| 收缩压 (水银柱/毫米) | 110 | 115 | 120 | 125 | 130 | 135 | 140 | 145 | … |
| 舒张压 (水银柱/毫米) | 70 | 73 | 75 | 78 | 80 | 73 | 85 | 88 | … |
分析 由题意知表格中的收缩压和舒张压形成一个等差数列和一个有两个等差数列交叉组成的数列.其中收缩压是一个公差是5的等差数列,舒张压是一个是有两个等差数列交叉组成的数列,公差分别是3和2.
解答 解:由题意知表格中的收缩压和舒张压形成一个等差数列和一个有两个等差数列交叉组成的数列,
其中收缩压是一个公差是5的等差数列,
∴135+5=140,
舒张压是一个是有两个等差数列交叉组成的数列,
∴85+3=88,
故答案为:140,88
点评 培养学生观察、分析、归纳、推理的能力;在领会函数与数列关系的前提下,把研究函数的方法迁移来研究数列,培养学生的知识、方法迁移能力.提高学生分析问题和解决问题的能力.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (?p)∧q | B. | (?p)∧(?q) | C. | p∨(¬q) | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
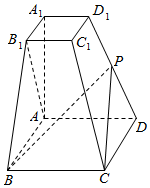 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,0] | B. | $[\frac{π}{12},\frac{7π}{12}]$ | C. | [0,$\frac{π}{3}$] | D. | [$\frac{π}{2}$,$\frac{5π}{6}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com