
���� ��I������C�ļ����귽��Ϊ��2=$\frac{12}{4co{s}^{2}��+3si{n}^{2}��}$����4��2cos2��+3��2sin2��=12����$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}\right.$����ɵ�����C��ֱ�����귽�̣�ֱ��l�IJ������̣�$\left\{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=2+\frac{\sqrt{3}}{2}t}{\;}\end{array}\right.$��tΪ����������ȥ����t��Ϊֱ��l����ͨ���̣�
�������ڵ�P��1��2����ֱ��l�ϣ���$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=2+\frac{{\sqrt{3}}}{2}t\end{array}\right.$����$\frac{x^2}{3}+\frac{y^2}{4}=1$�������ã�$13{t^2}+4��4+6\sqrt{3}��t+16=0$���跽�̵�����ʵ��Ϊt1��t2������t�ļ������弴�ɵó���
��� �⣺��I������C�ļ����귽��Ϊ��2=$\frac{12}{4co{s}^{2}��+3si{n}^{2}��}$����4��2cos2��+3��2sin2��=12���ɵã�����C��ֱ�����귽��Ϊ4x2+3y2=12����Ϊ$\frac{x^2}{3}+\frac{y^2}{4}=1$��
ֱ��l�IJ������̣�$\left\{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=2+\frac{\sqrt{3}}{2}t}{\;}\end{array}\right.$��tΪ����������ȥ����t��Ϊ��ֱ��l����ͨ����Ϊ$\sqrt{3}x-y-\sqrt{3}+2=0$��
���ߵ�P��1��2����ֱ��l�ϣ���$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=2+\frac{{\sqrt{3}}}{2}t\end{array}\right.$����$\frac{x^2}{3}+\frac{y^2}{4}=1$��
�����ã�$13{t^2}+4��4+6\sqrt{3}��t+16=0$������0��
�跽�̵�����ʵ��Ϊt1��t2����${t_1}+{t_2}=-\frac{{8��2+3\sqrt{3}��}}{13}$��
����t�ļ�������ã�$|{PA}|+|{PB}|=-��{t_1}+{t_2}��=\frac{{8��2+3\sqrt{3}��}}{13}$��
���� ���⿼���˼����껯Ϊֱ�����귽�̵ķ�����ֱ������Բ�ཻ�ҳ����⡢ֱ�߲������̵�Ӧ�ã�������������������������������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
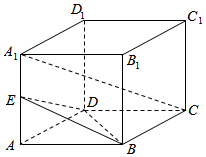 ��ͼ���ⳤΪ1��������ABCD-A1B1C1D1�У�E��AA1���е㣮
��ͼ���ⳤΪ1��������ABCD-A1B1C1D1�У�E��AA1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 4$\sqrt{3}$ | B�� | 4 | C�� | 6$\sqrt{3}$ | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 68 | B�� | 72 | C�� | 84 | D�� | 90 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x0��8 | B�� | 0��x0��1��x0��8 | C�� | 0��x0��8 | D�� | -1��x0��0��0��x0��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $2\sqrt{5}$ | B�� | $\sqrt{5}$ | C�� | 2 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���䣨�꣩ | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | �� |
| ����ѹ ��ˮ����/���ף� | 110 | 115 | 120 | 125 | 130 | 135 | 140 | 145 | �� |
| ����ѹ ��ˮ����/���ף� | 70 | 73 | 75 | 78 | 80 | 73 | 85 | 88 | �� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com