
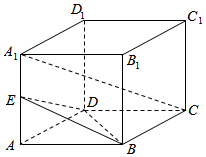
 如图,棱长为1的正方体ABCD-A1B1C1D1中,E是AA1的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1中,E是AA1的中点.分析 (1)连AC,设AC与BD交于点O,连EO,则A1C∥EO,由此能证明A1C∥平面BDE.
(2)由BD⊥AC,BD⊥EO,得∠AOE是二面角E-BD-A的平面角,由此能求出二面角E-BD-A的正切值.
解答  证明:(1)连AC,设AC与BD交于点O,连EO
证明:(1)连AC,设AC与BD交于点O,连EO
∵E是AA1的中点,O是BD的中点,∴A1C∥EO,
又EO?面BDE,AA1?面BDE,所以A1C∥平面BDE.…(6分)
解:(2)由(1)知,BD⊥AC,BD⊥EO,
∴∠AOE是二面角E-BD-A的平面角,
在Rt△AOE中,tan∠AOE=$\frac{AE}{AO}$=$\frac{\sqrt{2}}{2}$.
∴二面角E-BD-A的正切值为$\frac{\sqrt{2}}{2}$.…(12分)
点评 本题考查线面平行的证明,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-2,-1) | C. | (-3,-2) | D. | (-4,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -2 | C. | 2 | D. | log27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
| 空气质量 | 优 | 良 | 轻度污染 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 6 | 14 | 18 | 27 | 20 | 15 |
| 非重度污染 | 严重污染 | 合计 | |
| 供暖季 | 22 | 8 | 30 |
| 非供暖季 | 63 | 7 | 70 |
| 合计 | 85 | 15 | 100 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com