
| A. | (-2,0) | B. | (-2,-1) | C. | (-3,-2) | D. | (-4,-2) |
分析 ①根据平方的性质得到b+$\frac{1}{{3}^{a}}$-$\frac{1}{3}$=0且c-m(a2+a-m2-m)=0;②等价于对于任意a≥1,c<0,③等价于存在a<-1,使c>0,进而可求实数m的取值范围.
解答 解:①由①(b+$\frac{1}{{3}^{a}}$-$\frac{1}{3}$)2+[c-m(a2+a-m2-m)]2=0;
得b+$\frac{1}{{3}^{a}}$-$\frac{1}{3}$=0且c-m(a2+a-m2-m)=0;
即b=-$\frac{1}{{3}^{a}}$+$\frac{1}{3}$,c=m(a2+a-m2-m),
当a<1时,b=-$\frac{1}{{3}^{a}}$+$\frac{1}{3}$<0
当a≥1时,b≥0,
所以②等价于对于任意a≥1,c<0,③等价于存在a<-1,使c>0,
c=m(a2+a-m2-m)=m(a+$\frac{1}{2}$)2-$\frac{1}{4}$m-m(m2-m),
当a=1时c<0,
即m<0,且m+m-m2 (m+1)<0,
也即-2<m<0;
当存在a<-1,使c>0,时,
由以上知m<0,此时当a=-1时c>0,
即m-m-m2 (m+1)>0,得m<-1;
综上所述得-2<m<-1.
故选:B
点评 本题考查求实数m的取值范围,考查进行简单的合情推理,根据平方的性质以及不等式的性质进行转化是解决本题的关键.综合性较强,难度较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A?B | D. | B?A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 10 | 25 | 35 | 30 | x |
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 15 | 30 | 25 | y | 5 |
| 女士 | 男士 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
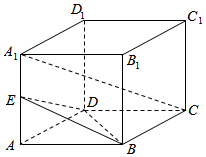 如图,棱长为1的正方体ABCD-A1B1C1D1中,E是AA1的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1中,E是AA1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com