
分析 (1)欲求椭圆C的方程和其“准圆”方程,只要求出半径$\sqrt{{a^2}+{b^2}}$即可,即分别求出椭圆方程中的a,b即得,这由题意不难求得;
(2)确定直线l的方程,代入椭圆方程并整理,利用韦达定理,结合$\overrightarrow{OC}$=λ($\overrightarrow{OA}$+$\overrightarrow{OB}$),求出C的坐标,代入椭圆方程,即可求λ的值.
(3)先分两种情况讨论:①当l1,l2中有一条无斜率时;②.②当l1,l2都有斜率时,第一种情形比较简单,对于第二种情形,将与椭圆只有一个公共点的直线为y=t(x-x0)+y0,代入椭圆方程,消去去y得到一个关于x的二次方程,根据根的判别式等于0得到一个方程:(3-x02)t2+2x0y0t+(x02-3)=0,而直线l1,l2的斜率正好是这个方程的两个根,从而证得l1⊥l2.
解答 解:(1)因为$c=\sqrt{2},a=\sqrt{3}$,所以b=1
所以椭圆的方程为$\frac{x^2}{3}+{y^2}=1$,
准圆的方程为x2+y2=4.
(2)过点(1,0)作一条倾斜角为30°的直线的方程为y=tan30°(x-1)=$\frac{\sqrt{3}}{3}$(x-1),
代入椭圆方程$\frac{x^2}{3}+{y^2}=1$,
并整理得x2-x-1=0.
设A(x1,y1),B(x2,y2),则x1+x2=1,
∴y1+y2=$\frac{\sqrt{3}}{3}$(x1-1)+$\frac{\sqrt{3}}{3}$(x2-1)=$\frac{\sqrt{3}}{3}$(x1+x2-2)=-$\frac{\sqrt{3}}{3}$.
∴$\overrightarrow{OC}$=λ($\overrightarrow{OA}$+$\overrightarrow{OB}$)=λ(x1+x2,y1+y2)=λ(1,-$\frac{\sqrt{3}}{3}$),
∴C点坐标为(λ,-$\frac{\sqrt{3}}{3}$λ),
代入椭圆方程$\frac{x^2}{3}+{y^2}=1$,可得$\frac{{λ}^{2}}{3}$+$\frac{{λ}^{2}}{3}$=1,
∴2λ2=3,解得λ=±$\frac{\sqrt{6}}{2}$.
(3)①当l1,l2中有一条无斜率时,不妨设l1无斜率,
因为l1与椭圆只有一个公共点,则其方程为$x=\sqrt{3}$或$x=-\sqrt{3}$,
当l1方程为$x=\sqrt{3}$时,此时l1与准圆交于点$(\sqrt{3},1)(\sqrt{3},-1)$,
此时经过点$(\sqrt{3},1)$(或$\sqrt{3},-1)$且与椭圆只有一个公共点的直线是y=1(或y=-1),
即l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可证l1方程为$x=-\sqrt{3}$时,直线l1,l2垂直.
②当l1,l2都有斜率时,设点P(x0,y0),其中x02+y02=4,
设经过点P(x0,y0),与椭圆只有一个公共点的直线为y=t(x-x0)+y0,
则$\left\{\begin{array}{l}y=tx+({y_0}-t{x_0})\\ \frac{x^2}{3}+{y^2}=1\end{array}\right.$,消去y得到x2+3(tx+(y0-tx0))2-3=0,
即(1+3t2)x2+6t(y0-tx0)x+3(y0-tx0)2-3=0,△=[6t(y0-tx0)]2-4•(1+3t2)[3(y0-tx0)2-3]=0,
经过化简得到:(3-x02)t2+2x0y0t+1-y02=0,因为x02+y02=4,所以有(3-x02)t2+2x0y0t+(x02-3)=0,
设l1,l2的斜率分别为t1,t2,因为l1,l2与椭圆都只有一个公共点,
所以t1,t2满足上述方程(3-x02)t2+2x0y0t+(x02-3)=0,
所以t1•t2=-1,即l1,l2垂直.
点评 本题主要考查了椭圆的标准方程、直线与圆锥曲线的综合问题,突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法,要求考生分析问题和解决问题的能力、计算能力较高.综合性较强,难度较大.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
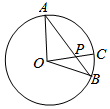 如图所示,点A,B,C是圆O上的三点,线段OC与线段AB交于圆内一点P,若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+2m$\overrightarrow{OB}$,$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,则λ=( )
如图所示,点A,B,C是圆O上的三点,线段OC与线段AB交于圆内一点P,若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+2m$\overrightarrow{OB}$,$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,则λ=( )| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | … |
| 收缩压 (水银柱/毫米) | 110 | 115 | 120 | 125 | 130 | 135 | 140 | 145 | … |
| 舒张压 (水银柱/毫米) | 70 | 73 | 75 | 78 | 80 | 73 | 85 | 88 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
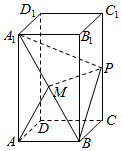 如图,正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.
如图,正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
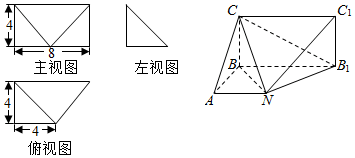
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
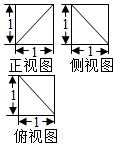
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com