
| A. | [-$\frac{π}{3}$,0] | B. | $[\frac{π}{12},\frac{7π}{12}]$ | C. | [0,$\frac{π}{3}$] | D. | [$\frac{π}{2}$,$\frac{5π}{6}$] |
分析 由周期求得ω,再根据正弦函数的减区间求得函数f(x)的单调减区间.
解答 解:函数f(x)=sin(ωx+$\frac{π}{3}$)(ω>0)相邻两个对称轴的距离为$\frac{π}{2}$,
∴$\frac{T}{2}$=$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{π}{2}$,解得ω=2;
∴f(x)=sin(2x+$\frac{π}{3}$);
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈Z,
∴2kπ+$\frac{π}{6}$≤2x≤2kπ+$\frac{7π}{6}$,k∈Z,
解得kπ+$\frac{π}{12}$≤x≤kπ+$\frac{7π}{12}$,k∈Z;
∴当k=0时,x∈[$\frac{π}{12}$,$\frac{7π}{12}$].
故选:B.
点评 本题主要考查正弦函数的图象和性质,正弦函数的减区间,属于基础题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:填空题
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | … |
| 收缩压 (水银柱/毫米) | 110 | 115 | 120 | 125 | 130 | 135 | 140 | 145 | … |
| 舒张压 (水银柱/毫米) | 70 | 73 | 75 | 78 | 80 | 73 | 85 | 88 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
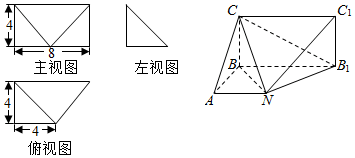
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
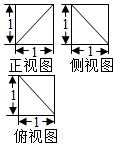
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6日和12日 | B. | 5日和6日 | C. | 1月和5月 | D. | 1月和11日 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com