
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
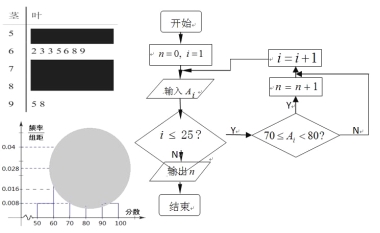
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
【答案】(Ⅰ)2,10,4(Ⅱ)众数75. 中位数73.5
【解析】
试题分析:(Ⅰ)由已知条件可知[50,60)之间的频率和频数可求得样本容易,结合频率分布直方图可得到各组频数;(Ⅱ)众数为出现次数最多的数,中位数为频率分布直方图中频率为0.5位置的数
试题解析:(Ⅰ)由直方图知:在[50,60)之间的频率为0.00810=0.08,
![]() 在[50,60)之间的频数为2;
在[50,60)之间的频数为2;
由程序框图知:在[70,80)之间的频数为10
所以分数在[80,90)之间的频数为25-2-7-10-2=4;
(Ⅱ)分数在[50,60)之间的频率为2/25=0.08;
分数在[60,70)之间的频率为7/25=0.28;
分数在[70,80)之间的频率为10/25=0.40;
分数在[80,90)之间的频率为4/25=0.16;
分数在[90,100]之间的频率为2/25=0.08;
估计该班的测试成绩的众数75. .....10分
设中位数为![]() ,则
,则![]() 得
得![]()


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于两点A,B,且![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
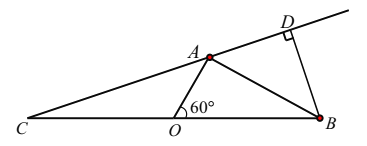
【题目】某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试。如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚![]() 秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
(1)求甲距燃放点C的距离;(2)求这种烟花的垂直“冲天”高度HC

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修,可供利用的旧墙足够长),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图2所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m, 设利用旧墙的长度为![]() (单位:
(单位: ![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元).
(单位:元).

(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个人连续射击三次,事件“至少有一次击中目标”的对立事件是( )
A.至多有一次击中目标B.三次都击不中目标
C.三次都击中目标D.只有一次击中目标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):

若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为3:2.
(1)试确定![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)试营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,则恰好选取1名“网购达人”和1名“非网购达人”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有![]() 三个旅游景点,在岸边
三个旅游景点,在岸边![]() 两地的中点处设有一个垃圾回收站点
两地的中点处设有一个垃圾回收站点![]() (如图),
(如图),![]() 两地相距10
两地相距10![]() ,从回收站
,从回收站![]() 观望
观望![]() 地和
地和![]() 地所成的视角为
地所成的视角为![]() ,且
,且![]() ,设
,设![]() ;
;
(1)用![]() 分别表示
分别表示![]() 和
和![]() ,并求出
,并求出![]() 的取值范围;
的取值范围;
(2)某一时刻太阳与![]() 三点在同一直线,此时
三点在同一直线,此时![]() 地到直线
地到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我国各景点在大众中的熟知度,随机对![]() ~
~![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组[ | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
![]()
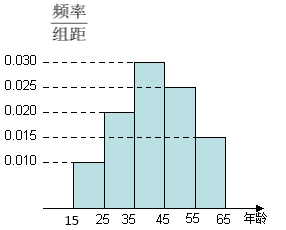
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组各抽取多少人;
组每组各抽取多少人;
(3)在(2)的条件下抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求所抽取的人中恰好没有第
人,求所抽取的人中恰好没有第![]() 组人的概率.
组人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com