
分析 由题意知本题是一个几何概型,以面积为测度,根据面积之比得到概率.
解答 解:由题意知本题是一个几何概型,
∵试验发生包含的所有事件对应的集合是Ω={x|80<x<120,60<y<120},
集合对应的面积是2400,
而满足条件的事件={x|80<x<120,60<y<120,|x-y|≤10},
对应的面积为2400-$\frac{1}{2}×30×30$-$\frac{(10+50)×40}{2}$=750,
∴两人能够会面的概率是$\frac{750}{2400}$=$\frac{5}{16}$,
故答案为$\frac{5}{16}$.
点评 本题主要考查几何概型的概率的计算,利用面积为测度是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1,1,0,0 | B. | 1,0,1,0 | C. | 0,1,0,1 | D. | 1,0,0,1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 13 | D. | $2\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | {x|x≥5} | C. | {x|x<3} | D. | {x|3<x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
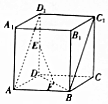 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com