
| A. | 周期为4π的奇函数 | B. | 周期为4π的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的非奇非偶函数 |
分析 根据函数y=Asin(ωx+∅)的图象变换规律可得f(x)=cos(2x-$\frac{π}{5}$),利用三角函数的图象和性质从而得解.
解答 解:由题意可得把函数 y=cosx 的图象的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),再把图象上所有点向右平行移动$\frac{π}{10}$个单位长度,
可得f(x)的图象,故 f(x)=cos2(x-$\frac{π}{10}$)=cos(2x-$\frac{π}{5}$),
可得:f(x)的周期T=$\frac{2π}{2}$=π.
由于f(0)=cos(-$\frac{π}{5}$)≠0,且f(0)=cos(-$\frac{π}{5}$)≠±1,故函数f(x)为非奇非偶函数,
故选:D.
点评 本题主要考查三角函数的图象和性质,函数y=Asin(ωx+∅)的图象变换,考查了数形结合思想,属于基础题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
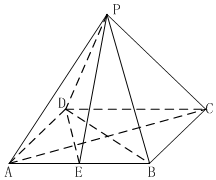 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1} | B. | {0,1,2} | C. | {-1,0,1,2} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-2) | B. | (-3,2) | C. | (2,4) | D. | (-2,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com