
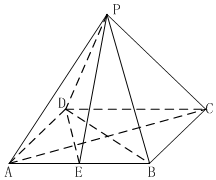
 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.分析 (1)先证明AC⊥DE由题可知面PAC⊥面ABCD,且交线为AC,可得DE⊥面PAC
(2取BC中点F,连接OE,OF,因为底面ABCD为矩形,所以OE⊥OF.建立如图所示的空间直角标系:A(1,-$\sqrt{2}$,0),B(1,$\sqrt{2}$,0),D(-1,-$\sqrt{2}$,0),P(0,0,a),$\overrightarrow{AP}=(-1,\sqrt{2},a)$,由PA与面PBD所成的角的正弦值为$\frac{\sqrt{6}}{3}$,得|$\overrightarrow{c}•\overrightarrow{AP}\$|=|$\overrightarrow{c}$|×|$\overrightarrow{AP}$|×$\frac{\sqrt{6}}{3}$,⇒a,再求出两个面的法向量即可.
解答 
解:(1)在矩形ABCD中,AB:BC=$\sqrt{2}:1$,且E是AB的中点,
∴tan∠ADE=tan∠CAB=$\frac{1}{\sqrt{2}}$,…(1分)
∴∠ADE=∠CAB,
∵∠CAB+∠DAC=90°,∴∠ADE+∠DAC=90°,即AC⊥DE.…(3分)
由题可知面PAC⊥面ABCD,且交线为AC,∴DE⊥面PAC.∴…(5分)
(2):令AC与BD交于点O,∵PA=PC,且O是AC的中点,∴PO⊥AC.
∵面PAC⊥面ABCD,∴PO⊥面ABCD.
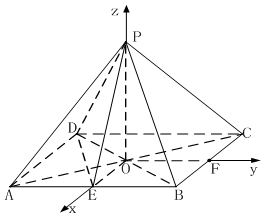
取BC中点F,连接OE,OF,因为底面ABCD为矩形,所以OE⊥OF.建立如图所示的空间直角标系:
A(1,-$\sqrt{2}$,0),B(1,$\sqrt{2}$,0),D(-1,-$\sqrt{2}$,0),P(0,0,a),$\overrightarrow{AP}=(-1,\sqrt{2},a)$…(6分)
设面PDB的法向量为$\overrightarrow{c}=({x}_{1},{y}_{1},{z}_{1})$,$\overrightarrow{DB}=(2,2\sqrt{2},0),\overrightarrow{OP}=(0,0,a)$
由$\left\{\begin{array}{l}{\overrightarrow{c}•\overrightarrow{DB}=2{x}_{1}+2\sqrt{2}{y}_{1}=0}\\{\overrightarrow{c}•\overrightarrow{OP}=a{z}_{1}=0}\end{array}\right.$,
令${x}_{1}=\sqrt{2}$,∴面PDB的法向量为$\overrightarrow{c}=(\sqrt{2},-1,0)$
由∵PA与面PBD所成的角的正弦值为$\frac{\sqrt{6}}{3}$,∴
|$\overrightarrow{c}•\overrightarrow{AP}\$|=|$\overrightarrow{c}$|×|$\overrightarrow{AP}$|×$\frac{\sqrt{6}}{3}$,⇒a=1
设平面PAD的法向量为$\overrightarrow{m}=({x}_{2},{y}_{2},{z}_{2})$,$\overrightarrow{AD}=(-2,0,0)$,$\overrightarrow{AP}=(-1,\sqrt{2},1)$
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=-2{x}_{2}=0}\\{\overrightarrow{m}•\overrightarrow{AP}=-{x}_{2}+\sqrt{2}{y}_{2}+{z}_{2}=0}\end{array}\right.$ 令y2=1
∴$\overrightarrow{m}=(0,-1,\sqrt{2})$
设平面PAB的法向量为$\overrightarrow n=({x_3},{y_3},{z_3})$,$\overrightarrow{AB}=(0,2\sqrt{2},0),\overrightarrow{AP}=(-1,\sqrt{2},1)$
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=2\sqrt{2}{y}_{3}=0}\\{\overrightarrow{n}•\overrightarrow{AP}=-{x}_{3}+\sqrt{3}{y}_{3}+{z}_{3}=0}\end{array}\right.$,令x3=1
∴$\overrightarrow{n}=(1,0,1)$ …(10分)
cosθ=$\frac{-\sqrt{2}}{\sqrt{3}×\sqrt{2}}=-\frac{\sqrt{3}}{3}$
∴二面角D-PA-B的余弦值为-$\frac{\sqrt{3}}{3}$ …(12分)
点评 本题考查了空间线面垂直的判定,利用向量处理线面角、二面角问题,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2017 | D. | -2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
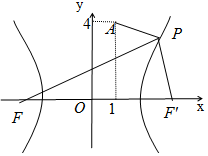 已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:
已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为4π的奇函数 | B. | 周期为4π的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com