
分析 (1)由$\overrightarrow{AP}$+$\overrightarrow{BP}$=λ($\overrightarrow{AQ}$+$\overrightarrow{BQ}$)(λ∈R,|λ|>1).得到$\overrightarrow{OP}$=λ$\overrightarrow{OQ}$,由此能证明点P,Q,O三点共线.
(2)设P(x1,y1),Q(x2,y2),求出k1+k2=$\frac{2{b}^{2}}{{a}^{2}}•\frac{{x}_{1}}{{y}_{1}}$,${k}_{3}+{k}_{4}=-\frac{2{b}^{2}}{{a}^{2}}•\frac{{x}_{2}}{{y}_{2}}$,由$\overrightarrow{OP}$=λ$\overrightarrow{OQ}$,能出k1+k2+k3+k4的值.
(3)由$\overrightarrow{OP}$=λ$\overrightarrow{OQ}$,推导出$\left\{\begin{array}{l}{{{x}_{1}}^{2}=\frac{{λ}^{2}+1}{2}{a}^{2}}\\{{{y}_{1}}^{2}=\frac{{λ}^{2}-1}{2}{b}^{2}}\end{array}\right.$,再由PF1∥QF2,得到(k1+k2)2=4,(k3+k4)2=4,由此能求出k12+k22+k32+k42的值.
解答 证明:(1)∵A、B为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$和双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的公共顶点,
P、Q分别为双曲线和椭圆上不同于A、B的动点,且$\overrightarrow{AP}$+$\overrightarrow{BP}$=λ($\overrightarrow{AQ}$+$\overrightarrow{BQ}$)(λ∈R,|λ|>1).
∴$\overrightarrow{OP}$=λ$\overrightarrow{OQ}$,
∴点P,Q,O三点共线.
解:(2)设P(x1,y1),Q(x2,y2),
则${k}_{1}+{k}_{2}=\frac{{y}_{1}}{{x}_{1}+a}+\frac{{y}_{1}}{{x}_{1}-a}$=$\frac{2{x}_{1}{y}_{1}}{{{x}_{1}}^{2}-{a}^{2}}$=$\frac{2{x}_{1}{y}_{1}}{\frac{{a}^{2}}{{b}^{2}}•{{y}_{1}}^{2}}$=$\frac{2{b}^{2}}{{a}^{2}}•\frac{{x}_{1}}{{y}_{1}}$,
同理,得:${k}_{3}+{k}_{4}=-\frac{2{b}^{2}}{{a}^{2}}•\frac{{x}_{2}}{{y}_{2}}$,
∵$\overrightarrow{OP}$=λ$\overrightarrow{OQ}$,∴x1=λx2,y1=λy2,
∴$\frac{{x}_{1}}{{y}_{1}}=\frac{{x}_{2}}{{y}_{2}}$,
∴k1+k2+k3+k4=$\frac{2{b}^{2}}{{a}^{2}}$($\frac{{x}_{1}}{{y}_{1}}-\frac{{x}_{2}}{{y}_{2}}$)=0.
(3)∵$\overrightarrow{OP}$=λ$\overrightarrow{OQ}$,∴$\left\{\begin{array}{l}{{x}_{2}=\frac{1}{λ}{x}_{1}}\\{{y}_{2}=\frac{1}{λ}{y}_{1}}\end{array}\right.$,
∵$\frac{{{x}_{2}}^{2}}{{a}^{2}}+\frac{{{y}_{2}}^{2}}{{b}^{2}}=1$,
∴$\frac{{{x}_{1}}^{2}}{{a}^{2}}+\frac{{{y}_{1}}^{2}}{{b}^{2}}$=λ2,又$\frac{{{x}_{1}}^{2}}{{a}^{2}}-\frac{{{y}_{1}}^{2}}{{b}^{2}}$=1,
∴$\left\{\begin{array}{l}{{{x}_{1}}^{2}=\frac{{λ}^{2}+1}{2}{a}^{2}}\\{{{y}_{1}}^{2}=\frac{{λ}^{2}-1}{2}{b}^{2}}\end{array}\right.$,
又∵PF1∥QF2,∴|OF1|=λ|OF2|,
∴λ2=$\frac{{a}^{2}+{b}^{2}}{{a}^{2}-{b}^{2}}$,
∴$\frac{{{x}_{1}}^{2}}{{{y}_{1}}^{2}}$=$\frac{{λ}^{2}+1}{{λ}^{2}-1}$•$\frac{{a}^{2}}{{b}^{2}}$=$\frac{{a}^{4}}{{b}^{4}}$,
∴(k1+k2)2=4•$\frac{{b}^{4}}{{a}^{4}}$•$\frac{{{x}_{1}}^{2}}{{{y}_{1}}^{2}}$=4•$\frac{{b}^{4}}{{a}^{4}}$•$\frac{{a}^{4}}{{b}^{4}}$=4,
同理(k3+k4)2=4,
k1•k2=$\frac{{y}_{1}}{{x}_{1}+a}$•$\frac{{y}_{1}}{{x}_{1}-a}$=$\frac{{{y}_{1}}^{2}}{{{x}_{1}}^{2}-{a}^{2}}$,且$\frac{{{x}_{1}}^{2}}{{a}^{2}}$-$\frac{{{y}_{1}}^{2}}{{a}^{2}}$=1,
∴x12-a2=$\frac{{a}^{2}}{{b}^{2}}$•y12,
∴k1k2=$\frac{{b}^{2}}{{a}^{2}}$同理k3k4=-$\frac{{b}^{2}}{{a}^{2}}$,
∴k12+k22+k32+k42=(k1+k2)2+(k3+k4)2-2(k1•k2+k3•k4)=4+4-0=8.
点评 本题考查圆锥曲线的综合,着重考查整体代换与方程思想,培养学生综合分析问题,解决问题的能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{4}$,+∞) | B. | (-∞,$\frac{3}{4}$) | C. | (0,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-1 | B. | x=0 | C. | $x=\frac{1}{2}$ | D. | $x=-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
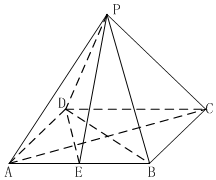 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{1}{4}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1} | B. | {0,1,2} | C. | {-1,0,1,2} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R,x02-x0≤0”的否定为“?x∈R,x2-x>0” | |
| B. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,则$\overrightarrow a$与$\overrightarrow b$共线 | |
| C. | 命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”的逆否命题为真命题 | |
| D. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com