
| A. | 命题“?x0∈R,x02-x0≤0”的否定为“?x∈R,x2-x>0” | |
| B. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,则$\overrightarrow a$与$\overrightarrow b$共线 | |
| C. | 命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”的逆否命题为真命题 | |
| D. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 |
分析 由特称命题的否定为全称命题,即可判断A;由向量共线的条件,即可判断B;由A=150°,可得sinA=$\frac{1}{2}$,再结合原命题与逆否命题等价,即可判断C;由a1<0,0<q<1,即可判断D.
解答 解:对于A,由特称命题的否定为全称命题,可得命题“?x0∈R,x02-x0≤0”
的否定为“?x∈R,x2-x>0”,故A错;
对于B,若非零向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$同向,则$\overrightarrow a$与$\overrightarrow b$共线,故B正确
对于C,命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”为假命题,比如A=150°,则sinA=$\frac{1}{2}$.
再由原命题与其逆否命题等价,则其逆否命题为假命题,故C错;
对于D,设{an}是公比为q的等比数列,则“q>1”推不出“{an}为递增数列”,比如a1<0,不为增函数;
反之,可得0<q<1.故不为充分必要条件,故D错.
故选:B.
点评 本题考查命题的真假判断,主要是命题的否定、四种命题的真假、充分必要条件的判断和向量共线的条件,考查判断和推理能力,属于基础题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{6}$ | B. | -$\frac{\sqrt{6}}{2}$ | C. | ±$\sqrt{6}$ | D. | ±$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
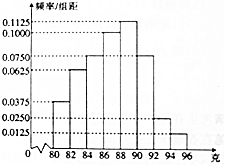 某仪器厂从新生产的一批零件中随机抽取40个检测,如图是根据抽样检测后零件的质量(单位:克)绘制的频率分布直方图,样本数据分8组,分别为[80,82),[82,84),[84,86),[86,88),[88,90),[90,92),[92,94),[94,96],则样本的中位数在( )
某仪器厂从新生产的一批零件中随机抽取40个检测,如图是根据抽样检测后零件的质量(单位:克)绘制的频率分布直方图,样本数据分8组,分别为[80,82),[82,84),[84,86),[86,88),[88,90),[90,92),[92,94),[94,96],则样本的中位数在( )| A. | 第3组 | B. | 第4组 | C. | 第5组 | D. | 第6组 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com