
分析 (1)根据考生的成绩ξ~N(90,100),得到正态曲线关于x=90对称,根据3σ原则知P(70<x<110)=P(90-2×10<x<90+2×10)=0.9544;
(2)P(80<x<100)=P(90-10<x<90+10)=0.683,即可得到结果.
解答 解:(1)∵考生的成绩ξ服从正态分布,即ξ~N(90,100),
∴正态曲线关于x=90对称,且标准差为10,
根据3σ原则知P(70<x<110)=P(90-2×10<x<90+2×10)=0.9544,
(2)P(80<x<100)=P(90-10<x<90+10)=0.683,
考试成绩X位于区间(80,100)上的概率为0.683,
则估计考试成绩在(80,100)间的考生大约有2000×0.683=1366人.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,解题的关键是注意利用正态曲线的对称性.


科目:高中数学 来源: 题型:解答题
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
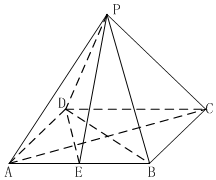 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com