
分析 对k分类讨论,利用一元二次不等式的解法求出已知不等式的解集确定出A,根据B=A∩Z(其中Z为整数集),集合B为有限集,即可得出.
解答 解:分情况考虑:①当k<0,A={x|$\frac{k}{4}$+$\frac{9}{4k}$+3<x<$\frac{11}{2}$};
②当k=0,A={x|x<$\frac{11}{2}$};
③当0<k<1或k>9,A={x|x<$\frac{11}{2}$,或x>$\frac{k}{4}$+$\frac{9}{4k}$+3};
④当1≤k≤9,A={x|x<$\frac{k}{4}$+$\frac{9}{4k}$+3,或x>$\frac{11}{2}$};
∵B=A∩Z(其中Z为整数集),集合B为有限集,
只有k<0,B={2,3,4,5}.
故答案为:{2,3,4,5}
点评 此题考查了交集及其运算,以及一元二次不等式的解法,考查了分类讨论方法、推理能力与计算能力,表示出解集A是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标伸长为原来的2倍 | |
| B. | 横坐标伸长为原来的2倍,纵坐标伸长为原来的2倍 | |
| C. | 横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标缩短为原来的$\frac{1}{2}$倍 | |
| D. | 横坐标伸长为原来的2倍,纵坐标缩短为原来的$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
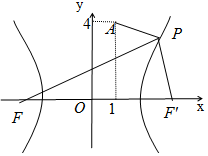 已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:
已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $81\sqrt{3}$ | B. | $27\sqrt{3}$ | C. | $9\sqrt{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
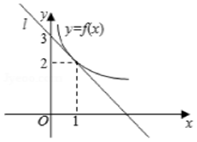 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com