
分析 (Ⅰ)求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,得到函数的单调区间,根据函数的单调性确定a的范围即可;
(Ⅲ)根据ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{2{(x}_{1}{-x}_{2})}{{{x}_{1}+x}_{2}}$=0,得到ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{2\frac{{x}_{1}}{{x}_{2}}-2}{\frac{{x}_{1}}{{x}_{2}}+1}$=0,设t=$\frac{{x}_{1}}{{x}_{2}}$(0<t<1),则lnt-$\frac{2t-2}{t+1}$=0,令u(t)=lnt-$\frac{2t-2}{t+1}$(0<t<1),根据函数的单调性证明即可.
解答 解:(I)f(x)定义域为(0,+∞),f′(x)=$\frac{1}{x}$+2ax-a=$\frac{2{ax}^{2}-ax+1}{x}$,
当a=-1时,f′(x)=$\frac{-(2x+1)(x-1)}{x}$,由f′(x)=0,∴x=-$\frac{1}{2}$或x=1,
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - |
| f(x) | 单调递增 | 极大值 | 单调递减 |
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想、转化思想,考查不等式的证明,是一道综合题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
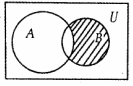
| A. | {x|-2≤x<4} | B. | {x|x≤2或x≥4} | C. | {x|-2≤x≤-1} | D. | {x|-1≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{14}}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | ±$\frac{\sqrt{14}}{3}$ | D. | ±$\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com