
分析 由题意可得,当x∈(-∞,1]时,$\frac{1+{2}^{x}+{3}^{x}+{4}^{x}•a}{4}$>0,即当x∈(-∞,1]时,a•4x+3x+2x+1>0,分离参数a,利用函数的单调性求出g(x)=-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上的最大值得答案.
解答 解:由题意可知,当x∈(-∞,1]时,$\frac{1+{2}^{x}+{3}^{x}+{4}^{x}•a}{4}$>0,
即当x∈(-∞,1]时,a•4x+3x+2x+1>0,
∴a>-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上恒成立.
∵函数g(x)=-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上为增函数,
∴$g(x)_{max}=g(1)=-\frac{3}{2}$.
∴$a>-\frac{3}{2}$.
故a的取值范围为($-\frac{3}{2},+∞$).
点评 本题考查函数的定义域及其求法,考查数学转化思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $81\sqrt{3}$ | B. | $27\sqrt{3}$ | C. | $9\sqrt{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为4π的奇函数 | B. | 周期为4π的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\frac{2}{17}$ | B. | 2$\frac{3}{17}$ | C. | 2$\frac{5}{17}$ | D. | 2.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
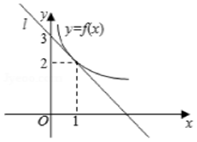 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com