Question

9．函数y=|log₃x|的图象与直线l₁：y=m从左至右分别交于点A，B，与直线${l_2}：y=\frac{8}{2m+1}（m＞0）$从左至右分别交于点C，D．记线段AC和BD在x轴上的投影长度分别为a，b，则$\frac{b}{a}$的最小值为（　　）

• A． $81\sqrt{3}$
• B． $27\sqrt{3}$
• C． $9\sqrt{3}$
• D． $3\sqrt{3}$

Answer 1

分析 依题意可求得A，B，C，D的横坐标值，得$\frac{b}{a}$=$\frac{|{3}^{m}-{3}^{\frac{8}{2m+1}|}}{|{3}^{-m}-{3}^{-\frac{8}{2m+1}}|}$=${3}^{m+\frac{8}{2m+1}}$，利用基本不等式可求最小值．

解答 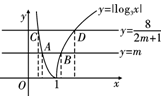解：在同一坐标系中作出y=m，y=$\frac{8}{2m+1}$（m＞0），y=|log₃x|的图象，如图，设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），D（x₄，y₄），
由|log₃x|=m，得x₁=3^-m，x₂=3^m，
由log₃x|=$\frac{8}{2m+1}$，得x₃=${3}^{-\frac{8}{2m+1}}$，x₄=${3}^{\frac{8}{2m+1}}$．
依照题意得$\frac{b}{a}$=$\frac{|{3}^{m}-{3}^{\frac{8}{2m+1}|}}{|{3}^{-m}-{3}^{-\frac{8}{2m+1}}|}$=${3}^{m+\frac{8}{2m+1}}$，
又m＞0，∴m+$\frac{8}{2m+1}$=$\frac{1}{2}$（2m+1）+$\frac{8}{2m+1}$-$\frac{1}{2}$≥$\frac{7}{2}$，
当且仅当$\frac{1}{2}$（2m+1）=$\frac{8}{2m+1}$，即m=$\frac{3}{2}$时取“=”号，
∴$\frac{b}{a}$的最小值为27$\sqrt{3}$，
故选B．

点评 本题考查对数函数图象与性质的综合应用，理解投影的概念并能把问题转化为基本不等式求最值是解决问题的关键，属中档题．