Question

14．已知直线l：ax+2by+3c=0和两定点A（0，13），B（5，10），若点B在l上的射影为C，且a，2b，3c成等差数列，则|AC|的取值范围为[$\sqrt{10}$，5$\sqrt{10}$]．

Answer 1

分析 运用等差数列中项的性质，结合直线方程可得直线恒过定点（1，-2），讨论直线l的斜率不存在和为0，求得C的 坐标，运用两点的距离公式，即可得到所求最值，进而得到所求范围．

解答 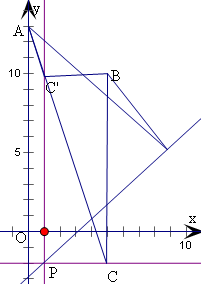解：a，2b，3c成等差数列，
可得a-4b+3c=0，
即有直线l：ax+2by+3c=0恒过定点P（1，-2），
若点B在l上的射影为C，
当直线l的斜率不存在，即方程为x=1，
可得C（1，10），
|AC|取得最小值为$\sqrt{（0-1）^{2}+（13-10）^{2}}$=$\sqrt{10}$；
当直线l的斜率为0，即方程为y=-2，
可得C（5，-2），
|AC|取得最大值为$\sqrt{（0-5）^{2}+（13+2）^{2}}$=5$\sqrt{10}$．
则|AC、的取值范围是[$\sqrt{10}$，5$\sqrt{10}$]．
故答案为：[$\sqrt{10}$，5$\sqrt{10}$]．

点评 本题考查线段长的取值范围，注意运用旋转运动思想，同时考查等差数列的中项的性质，以及直线恒过定点求法，考查运算能力和数形结合思想方法，属于中档题．