
| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
分析 根据椭圆的光学性质可知,当静止的小球放在点A处,从点A沿直线出发,射到左顶点,经椭圆壁反弹后,再回到点A时,小球经过的路程是2(a-c);射到右顶点,经椭圆壁反弹后,再回到点A时,小球经过的路程是2(a+c);小球从点A沿直线出发,经椭圆壁反弹到B点继续前行碰椭圆壁后回到A点,所走的轨迹正好是两次椭圆上的点到两焦点距离之和4a,进而根据椭圆的定义可求得小球经过的最长路程.
解答 解:依题意可知$\frac{x^2}{16}+\frac{y^2}{9}$=1中,a=4,b=3,c=$\sqrt{7}$,设A,B分别为左、右焦点,
则当静止的小球放在点A处,从点A沿直线出发,射到左顶点,经椭圆壁反弹后,
再回到点A时,小球经过的路程是2(a-c)=2(2-$\sqrt{7}$);
射到右顶点,经椭圆壁反弹后,再回到点A时,小球经过的路程是2(a+c)=2(2+$\sqrt{7}$);
小球经两次椭圆壁后反弹后回到A点,根据椭圆的性质可知所走的路程正好是4a=4×4=16,
小球经过的最长路程16,
故选C.
点评 本题主要考查了椭圆的应用.解题的关键是利用了椭圆的第一定义,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
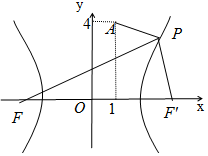 已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:
已知F是双曲线C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦点,A(1,4),P是双曲线右支上的动点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\frac{2}{17}$ | B. | 2$\frac{3}{17}$ | C. | 2$\frac{5}{17}$ | D. | 2.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com