
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA= ![]() ,E为BC的中点.
,E为BC的中点. 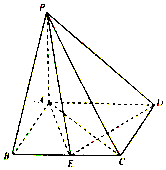
(1)证明:PE⊥ED;
(2)求二面角E﹣PD﹣A的大小.
【答案】
(1)证明:如图,
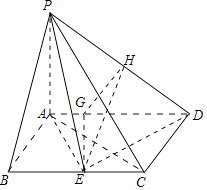
在△ABC中,∵AB=1,BC=2,AB⊥AC,
∴cosB= ![]() ,
, ![]() B=60°,又E为BC的中点,
B=60°,又E为BC的中点,
∴△ABE为正三角形,则AE=1,
在△AED中,∵AE=1,AD=2,∠EAD=60°,
∴ ![]() ,
,
∴AE2+ED2=AD2,则AE⊥ED.
又PA⊥平面ABCD,∴PA⊥ED,
∵PA∩AE=A,∴ED⊥平面PAE,则PE⊥ED;
(2)解:∵PA⊥平面ABCD,∴平面PAD⊥平面ABCD,
过E作EG⊥AD,垂足为G,则EG⊥平面PAD,∴EG⊥PD,
过G作GH⊥PD,垂足为H,连接EH,
∴PD⊥平面EGH,则PD⊥EH.
则∠EHG为二面角E﹣PD﹣A的平面角.
在Rt△AED中,由AE=1,AD=2,ED= ![]() ,可得EG=
,可得EG= ![]() ,
,
∴GD= ![]() ,
,
由△PAD∽△GHD,可得 ![]() ,即GH=
,即GH= 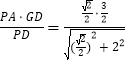 =
= ![]() .
.
∴tan 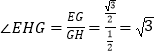 ,即∠EHG=60°.
,即∠EHG=60°.
∴二面角E﹣PD﹣A的大小为60°
【解析】(1)在△ABC中,由题意可得△ABE为正三角形,则AE=1,在△AED中,求解三角形可得AE⊥ED.然后利用线面垂直的判定可得ED⊥平面PAE,从而得到PE⊥ED;(2)由PA⊥平面ABCD,得平面PAD⊥平面ABCD,然后找出二面角E﹣PD﹣A的平面角.求解三角形可得二面角E﹣PD﹣A的大小.
【考点精析】通过灵活运用空间中直线与直线之间的位置关系,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点即可以解答此题.


科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的最高点D的坐标(
)的最高点D的坐标( ![]() ,2),由D点运动到相邻最低点时函数曲线与x轴的交点(
,2),由D点运动到相邻最低点时函数曲线与x轴的交点( ![]() ,0)
,0)
(1)求f(x)的解析式
(2)求f(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在区间[ ![]() ,2]上,函数f(x)=x2+px+q与g(x)=2x+
,2]上,函数f(x)=x2+px+q与g(x)=2x+ ![]() 在同一点取得相同的最小值,那么f(x)在[
在同一点取得相同的最小值,那么f(x)在[ ![]() ,2]上的最大值是( )
,2]上的最大值是( )
A.![]()
B.![]()
C.8
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?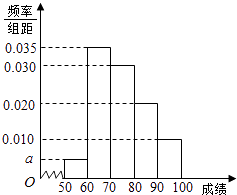
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com