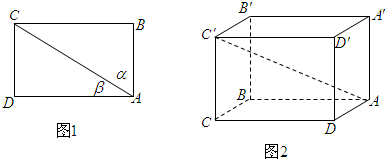
解:有如下命题:长方体ABCD-A'B'C'D'中,对角线AC'与棱AB、AD、AA'所成的角分别为α,β,γ,则cos
2α+cos
2β+cos
2γ=1…(4分)
证明:∵
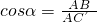
,
K^S*5U.C#O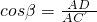
,
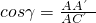
…(10分)
∴
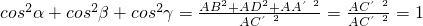
…(13分)
此题答案不唯一,只要类比写出的命题为真并证明,都应给相应的分数
分析:本题考查的知识点是类比推理,由在长方形中,设一条对角线与其一顶点出发的两条边所成的角分别是α,β,则有cos
2α+cos
2β=1,我们根据平面性质可以类比推断出空间性质,我们易得答案.
点评:本题考查的知识点是类比推理,在由平面图形的性质向空间物体的性质进行类比时,常用的思路有:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中面的性质类比推理出空间中体的性质,或是将平面中的两维性质,类比推断到空间中的三维性质.

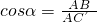 ,K^S*5U.C#O
,K^S*5U.C#O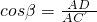 ,
,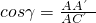 …(10分)
…(10分)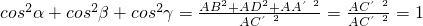 …(13分)
…(13分)
