
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
),过点P(2,1)的直线l与椭圆C相交于不同的两点A,B.
(1)求椭圆C的方程;
(2)是否存在直线l,满足![]() ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】试题分析(1)先设椭圆的标准方程,将点![]() 代入得到一个方程,根据离心率得到一个关系式,再由
代入得到一个方程,根据离心率得到一个关系式,再由![]() 可得到
可得到![]() 的值,进而得到椭圆的方程.(2)假设存在直线满足条件,设直线方程为
的值,进而得到椭圆的方程.(2)假设存在直线满足条件,设直线方程为![]() ,然后与椭圆方程联立消去
,然后与椭圆方程联立消去![]() 得到一元二次方程,且方程一定有两根,故应
得到一元二次方程,且方程一定有两根,故应![]() 大于
大于![]() 得到
得到![]() 的范围,进而可得到两根之和、两根之积的表达式,再表示出
的范围,进而可得到两根之和、两根之积的表达式,再表示出![]() ,再代入关系式
,再代入关系式![]() 可确定
可确定![]() 的值,从而得解.
的值,从而得解.
试题解析:(1)设椭圆C的方程为![]() ,
,
由题意得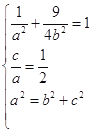 解得
解得![]() .故椭圆C的方程为
.故椭圆C的方程为![]() .
.
(2)若存在直线l满足条件,由题意可设直线l的方程为![]() ,由
,由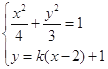
得![]() .
.
因为直线l与椭圆C相交于不同的两点A,B,
设A,B两点的坐标分别为![]() ,
,
所以![]()
整理得![]() ,解得
,解得![]() .
.
又![]() ,
,![]() ,且
,且![]()
即![]() ,
,
所以![]() ,
,
即![]() .
.
所以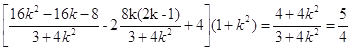 ,
,
解得![]() .
.
所以k=![]() .于是存在直线l满足条件,
.于是存在直线l满足条件,
其方程为![]() .
.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】下列推理不属于合情推理的是( )
A. 由铜、铁、铝、金、银等金属能导电,得出一切金属都能导电.
B. 半径为![]() 的圆面积
的圆面积![]() ,则单位圆面积为
,则单位圆面积为![]() .
.
C. 由平面三角形的性质推测空间三棱锥的性质.
D. 猜想数列2,4,8,…的通项公式为![]() .
. ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一个总体的100个个体编号为0,1,2,…,99,并依次将其分为10个组,组号为0,1,2,…,9.要用系统抽样法抽取一个容量为10的样本,如果在第0组(号码为0—9)随机抽取的号码为2,则抽取的10个号码为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=![]() ,其中2<m<2,m∈Z,满足:
,其中2<m<2,m∈Z,满足:
(1)f(x)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(x) +f(x)=0.
求同时满足条件(1)、(2)的幂函数f(x)的解析式,并求x∈[0,3]时,f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点,焦点在![]() 轴上的椭圆,下顶点
轴上的椭圆,下顶点![]() ,且离心率
,且离心率![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点.在
两点.在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数不超过20人,每人需交费用800元;若旅行团人数超过20人,则给予优惠:每多1人,人均费用减少10元,直到达到规定人数60人为止.旅行社需支付各种费用共计10000元.
(1)写出每人需交费用S关于旅行团人数![]() 的函数;
的函数;
(2)旅行团人数x为多少时,旅行社可获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com