
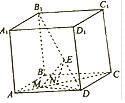
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1.分析 (1)证明MN⊥平面DEN,求出三角形DEN的面积,代入体积公式计算即可;
(2)根据体积求出E到平面ABCD的距离,再利用相似三角形求出DE.
解答 解:(1)∵底面ABCD是边长为2的正方形,N是AC的中点,
∴AC⊥BD,DN=$\sqrt{2}$,
∵BB1⊥平面ABCD,AC?平面ABCD,
∴AC⊥BB1,又BB1∩BD=B,
∴AC⊥平面BB1D,
故当N为AC的中点时,有MN⊥平面DEN,
又DB1=2$\sqrt{3}$,BB1=2,∴sin∠BDB1=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴VE-DMN=VM-DEN=$\frac{1}{3}{S}_{△DEN}•MN$=$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\frac{\sqrt{3}}{3}×1$=$\frac{\sqrt{3}}{9}$.
(2)设三棱锥E-DMN的高为h,
则VE-DMN=$\frac{1}{3}{S}_{△DMN}•h$=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{2}×h$=$\frac{\sqrt{2}h}{6}$=$\frac{1}{3}$,
∴h=$\sqrt{2}$,
∵$\frac{h}{B{B}_{1}}=\frac{DE}{D{B}_{1}}$,即$\frac{\sqrt{2}}{2}=\frac{DE}{2\sqrt{3}}$,∴DE=$\sqrt{6}$.
故答案为:(1)$\frac{\sqrt{3}}{9}$,(2)$\sqrt{6}$.
点评 本题考查线面位置关系的判断,棱锥的体积计算,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{17}{24}$ | D. | -$\frac{17}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{5}{12},\frac{11}{24}}]$ | B. | $({0,\frac{5}{12}}]∪[{\frac{11}{24},\frac{1}{2}})$ | C. | $({0,\frac{1}{2}})$ | D. | $({0,\frac{5}{24}}]∪[{\frac{5}{12},\frac{11}{24}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
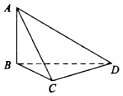 在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 24 | C. | 16 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com