
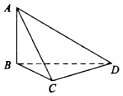
 在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 如图所示,分别取AB,AD,BC,BD的中点E,F,G,O,则EF∥BD,EG∥AC,FO⊥OG,∠FEG为异面直线AC与BD所成角.
解答 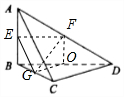 解:如图所示,分别取AB,AD,BC,BD的中点E,F,G,O,则EF∥BD,EG∥AC,FO⊥OG,
解:如图所示,分别取AB,AD,BC,BD的中点E,F,G,O,则EF∥BD,EG∥AC,FO⊥OG,
∴∠FEG为异面直线AC与BD所成角.
设AB=2a,则EG=EF=$\sqrt{2}$a,FG=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}$a,
∴∠FEG=60°,
∴异面直线AC与BD所成角的余弦值为$\frac{1}{2}$,
故选:A.
点评 本题考查异面直线AC与BD所成角,考查学生的计算能力,正确作出异面直线AC与BD所成角是关键.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1] | C. | (-1,1] | D. | (-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
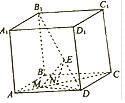 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为对角线B1D上的一点,M,N为对角线AC上的两个动点,且线段MN的长度为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | (1,5) | C. | (3,6) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
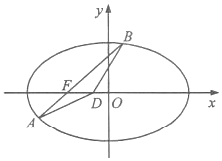 在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-1,0),且经过点(1,$\frac{3}{2}$).
在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-1,0),且经过点(1,$\frac{3}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com