练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知奇函数f（x）的定义域为R，若f（x+1）为偶函数，且f（1）=1，则f（2016）+f（2015）=（　　）
    A．-2B．1C．0D．-1

    分析 根据f（x）和f（x+1）的奇偶性便可得到f（x）=f（x-1+1）=f（x-4），从而得出f（x）是周期为4的周期函数，而可以求出f（2）=0，从而可以得出f（2016）+f（2015）=f（2）-f（1）=-1．

    解答 解：∵f（x）为R上的奇函数，f（x+1）为偶函数，
    ∴f（x）=f（x-1+1）=f（-x+2）=-f（x-2）=f（x-4）；
    ∴f（x）是周期为4的周期函数；
    ∴f（2016）+f（2015）=f（2+503×4）+f（-1+504×4）=f（2）-f（1）=f（2）-1；
    f（-1+1）=f（1+1）=0；
    即f（2）=0；
    ∴f（2014）+f（2015）=0-1=-1．
    故选：D．

    点评 考查奇函数、偶函数的定义，以及周期函数的定义，清楚偶函数的定义：f（-x）=f（x），是自变量换上-x后函数值不变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

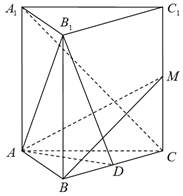    9．在正三棱柱ABC-A1B1C1中，AA1=2AB，点D是BC的中点，点M在CC1上，且$CM=\frac{1}{8}C{C_1}$．
    （1）求证：A1C∥平面AB1D；
    （2）求证：平面AB1D⊥平面ABM．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．在直四棱柱ABCD-A1B1C1D1中，底面ABCD为菱形，E，F分别是BB1，DD1的中点，G为AE的中点且FG=3，则△EFG的面积的最大值为（　　）
    A．$\frac{3}{2}$B．3C．$2\sqrt{3}$D．$\frac{{9\sqrt{3}}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知函数$f（x）=sin2ωx-2\sqrt{3}{cos^2}ωx+1（ω＞0）$在区间（π，2π）内没有极值点，则ω的取值范围为（　　）
    A．$（{\frac{5}{12}，\frac{11}{24}}]$B．$（{0，\frac{5}{12}}]∪[{\frac{11}{24}，\frac{1}{2}}）$C．$（{0，\frac{1}{2}}）$D．$（{0，\frac{5}{24}}]∪[{\frac{5}{12}，\frac{11}{24}}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知函数满足一下两个条件：①任意x1，x2∈（0，+∞），且x1≠x2时，（x1-x2）[f（x1）-f（x2）]＜0；②对定义域内任意x有f（x）+f（-x）=0，则符合条件的函数是（　　）
    A．f（x）=2xB．f（x）=1-|x|C．$f（x）=\frac{1}{x}-x$D．f（x）=ln（x+1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．设函数f（x）=2x+$\frac{1}{x}$的图象为C1，将C1向右平移2个单位，再向上平移4个单位得到图象C2，C2对应的函数为g（x）．
    （1）求g（x）的解析式与值域；
    （2）若直线y=x+m与C2有两个不同的交点，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知x≥0，求证：x≥sinx．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

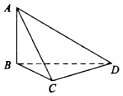    7．在我国古代数学名著《九章算术》中，将四个面都为直角三角形的四面体称为鳖臑，如图，在鳖臑ABCD中，AB⊥平面BCD，且AB=BC=CD，则异面直线AC与BD所成角的余弦值为（　　）
    A．$\frac{1}{2}$B．-$\frac{1}{2}$C．$\frac{\sqrt{3}}{2}$D．-$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知曲线C1：y=ex上一点A（x1，y1），曲线C2：y=1+ln（x-a）（a＞0）上一点B（x2，y2），当y1=y2时，对任意的x1，x2，都有|AB|≥e，则a的最小值为e-1．

    查看答案和解析>>

    同步练习册答案