
| A. | $\frac{3}{2}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
分析 建立坐标系,使用向量法求出E到直线FG的距离,代入面积公式,使用不等式的性质求出最值.
解答 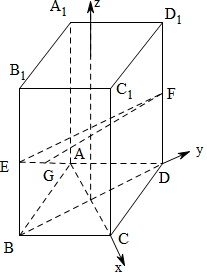 解:连接AC交BD于O,
解:连接AC交BD于O,
∵底面ABCD是菱形,∴AC⊥BD,
以OC,OD,OZ为坐标轴建立空间直角坐标系O-xyz,
设OC=a,OD=b,棱柱的高为h,
则A(-a,0,0),E(0,-b,$\frac{h}{2}$),F(0,b,$\frac{h}{2}$),∴G(-$\frac{a}{2}$,-$\frac{b}{2}$,$\frac{h}{4}$).
$\overrightarrow{FG}$=(-$\frac{a}{2}$,-$\frac{3b}{2}$,-$\frac{h}{4}$),$\overrightarrow{FE}$=(0,-2b,0),
∴cos<$\overrightarrow{FG},\overrightarrow{FE}$>=$\frac{\overrightarrow{FG}•\overrightarrow{FE}}{|\overrightarrow{FG}|•|\overrightarrow{FE}|}$=$\frac{3{b}^{2}}{3•2b}$=$\frac{b}{2}$,
∴E到直线FG的距离d=|$\overrightarrow{FE}$|sin<$\overrightarrow{FG},\overrightarrow{FE}$>=2b•$\frac{\sqrt{4-{b}^{2}}}{2}$=b$\sqrt{4-{b}^{2}}$,
∴S△EFG=$\frac{1}{2}•FG•d$=$\frac{3}{2}b\sqrt{4-{b}^{2}}$=$\frac{3}{2}\sqrt{{b}^{2}(4-{b}^{2})}$≤$\frac{3}{2}$×$\frac{{b}^{2}+4-{b}^{2}}{2}$=3.当且仅当b2=4-b2即b2=2时取等号.
故选:B.
点评 本题考查了空间向量与空间距离的计算,不等式的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1] | C. | (-1,1] | D. | (-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com