
分析 (1)由$lnx+\frac{a}{x}-1>-x+1$,(x>0),得a>-x2-xlnx+2x,令g(x)=-x2-xlnx+2x,则g′(x)=-2x-lnx+1,g''(x)=-$\frac{2x+1}{x}<0$,x∈[1,+∞),从而得到g(x)在[1,+∞)上单调递减,由此能求出a的取值范围.
(2)$\frac{f(x)}{x}$=$\frac{xlnx+a-x}{{x}^{2}}$,g′(x)=$\frac{2x-xlnx-2a}{{x}^{3}}$,由g′(x)=0,得2a=x-xlnx,令h(x)=x-xlnx,则h′(x)=-lnx<0,x∈[1,e2],由此推导出g(x)在[1,e2]上不存在极值.
解答 解:(1)∵f(x)=lnx+$\frac{a}{x}$-1,a∈R.
关于x的不等式f(x)>-x+1在[1,+∞)上恒成立,
∴$lnx+\frac{a}{x}-1>-x+1$,(x>0),
∴$\frac{a}{x}>-x-lnx+2$,∴a>-x2-xlnx+2x,
令g(x)=-x2-xlnx+2x,
则g′(x)=-2x-lnx-1+2
=-2x-lnx+1,
g''(x)=-2-$\frac{1}{x}$=-$\frac{2x+1}{x}<0$,x∈[1,+∞),
∴g′(x)单调递减,又g′(1)=-1,
∴g′(x)<0,x∈[1,+∞),
∴g(x)在[1,+∞)上单调递减,
g(x)max=g(1)=1,
∴a>1,即a的取值范围是[1,+∞).
(2)$\frac{f(x)}{x}$=$\frac{lnx}{x}+\frac{a}{{x}^{2}}-\frac{1}{x}$=$\frac{xlnx+a-x}{{x}^{2}}$,
g′(x)=$\frac{[lnx+1-1]{x}^{2}-2x(xlnx+a-x)}{({x}^{2})^{2}}$=$\frac{2x-xlnx-2a}{{x}^{3}}$,
由g′(x)=0,得2x-xlnx-2a=0,即2a=x-xlnx,
令h(x)=x-xlnx,
则h′(x)=1-lnx-1=-lnx<0,x∈[1,e2],
∴h(x)在[1,e2]上单调递减,
h(x)∈[-e2,1],又a>1,2a>2,∴2a≠x-xlnx,x∈[1,e2],
∴g(x)在[1,e2]上不存在极值.
点评 本题考查、实数的取值范围、导数性质、构造法等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想、分类与整合思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
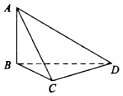 在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 24 | C. | 16 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com