
【题目】已知圆C的参数方程为 ![]() (θ为参数),若P是圆C与x轴的交点,以原点O为极点,x轴的正半轴为极轴建立极坐标系,设过点P的圆C的切线为l (Ⅰ)求直线l的极坐标方程
(θ为参数),若P是圆C与x轴的交点,以原点O为极点,x轴的正半轴为极轴建立极坐标系,设过点P的圆C的切线为l (Ⅰ)求直线l的极坐标方程
(Ⅱ)求圆C上到直线ρ(cosθ+ ![]() sinθ)+6=0的距离最大的点的直角坐标.
sinθ)+6=0的距离最大的点的直角坐标.
【答案】解:(Ⅰ)∵圆C的参数方程为 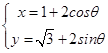 (θ为参数),
(θ为参数),
∴圆C的参数方程消去参数θ,得圆C的普通方程为(x﹣1)2+(y﹣ ![]() )2=4,
)2=4,
∵P是圆C与x轴的交点,以原点O为极点,x轴的正半轴为极轴建立极坐标系,设过点P的圆C的切线为l
由题设知,圆心C(1, ![]() ),P(2,0),
),P(2,0),
∠CPO=60°,故过P点的切线的倾斜角为30°,
设M(ρ,θ)是过P点的圆C的切线上的任一点,
则在△PMO中,∠MOP=θ,∠OMP=30°﹣θ,∠OPM=150°,
由正弦定理得 ![]() ,
,
∴ ![]() ,
,
∴直线l的极坐标方程为ρcos(θ+60°)=1.
(Ⅱ)∵直线ρ(cosθ+ ![]() sinθ)+6=0,
sinθ)+6=0,
∴直线的直角坐标方程为x+ ![]() y+6=0,
y+6=0,
设圆上的点M(1+2cosθ, ![]() ),
),
点M到直线的距离:
d= 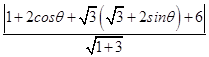 =
= ![]() ,
,
∴当θ= ![]() 时,点M到直线的距离取最大值
时,点M到直线的距离取最大值 ![]() .此时M(2,2
.此时M(2,2 ![]() ),
),
∴圆C上到直线ρ(cosθ+ ![]() sinθ)+6=0的距离最大的点的直角坐标为(2,2
sinθ)+6=0的距离最大的点的直角坐标为(2,2 ![]() ).
).
【解析】(Ⅰ)圆C的参数方程消去参数θ,得圆C的普通方程为(x﹣1)2+(y﹣ ![]() )2=4,由题设知,圆心C(1,
)2=4,由题设知,圆心C(1, ![]() ),P(2,0),过P点的切线的倾斜角为30°,设M(ρ,θ)是过P点的圆C的切线上的任一点,由正弦定理得
),P(2,0),过P点的切线的倾斜角为30°,设M(ρ,θ)是过P点的圆C的切线上的任一点,由正弦定理得 ![]() ,由此能求出直线l的极坐标方程.(Ⅱ)直线的直角坐标方程为x+
,由此能求出直线l的极坐标方程.(Ⅱ)直线的直角坐标方程为x+ ![]() y+6=0,设圆上的点M(1+2cosθ,
y+6=0,设圆上的点M(1+2cosθ, ![]() ),求出点M到直线的距离d=
),求出点M到直线的距离d= ![]() ,当θ=
,当θ= ![]() 时,点M到直线的距离取最大值,由此能求出圆C上到直线ρ(cosθ+
时,点M到直线的距离取最大值,由此能求出圆C上到直线ρ(cosθ+ ![]() sinθ)+6=0的距离最大的点的直角坐标.
sinθ)+6=0的距离最大的点的直角坐标.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+1(a∈R).
(1)若函数f(x)的图象在x=1处的切线l垂直于直线y=x,求实数a的值及直线l的方程;
(2)求函数f(x)的单调区间;
(3)若x>1,求证:lnx<x﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆 ![]() =1(a>b>0),F1、F2分别为椭 圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B、
=1(a>b>0),F1、F2分别为椭 圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B、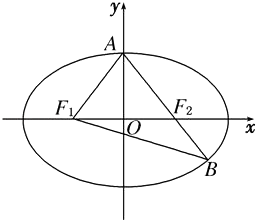
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若 ![]() =2
=2 ![]() ,
, ![]()
![]() =
= ![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图、正视图、侧视图、俯视图如图,M,N分别为A1B,B1C1的中点.
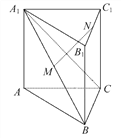
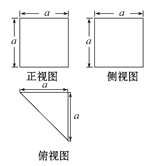
下列结论中正确的个数有 ( )
①直线MN与A1C相交.
②MN⊥BC.
③MN∥平面ACC1A1.
④三棱锥N-A1BC的体积为![]() =
=![]() a3.
a3.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=90°,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG.
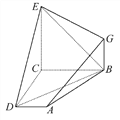
(1)求证:EC⊥CD.
(2)求证:AG∥平面BDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县相邻两镇在一平面直角坐标系下的坐标为A(1,2)、B(4,0),一条河所在直线方程为l:x+2y-10=0,若在河边l上建一座供水站P使之到A、B两镇的管道最省,问供水站P应建在什么地方?此时|PA|+|PB|为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com