
分析 由题意画出图形,由图形中所给的位置关系,逐一判断(1)、(2)、(3),利用等积法求出四面体A-BCD的内切球半径判断(4).
解答 解:根据题意,画出图形,如图所示: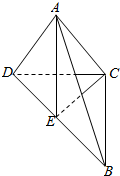
二面角A-BD-C为90°,E是BD的中点,可以得出∠AEC=90°,为直二面角的平面角;
对于(1),由于BD⊥面AEC,得出AC⊥BD,命题(1)正确;
对于(2),在等腰直角三角形AEC中,可以求出AC=$\sqrt{2}$AE=AD=CD,
所以△ACD是等边三角形,命题(2)正确;
对于(3),四面体ABCD的表面积为
S=2S△ACD+2S△ABD=2×$\frac{1}{2}$×12×sin60°+2×$\frac{1}{2}$×1×1=$\frac{\sqrt{3}}{2}$+1,
命题(3)正确;
对于(4),由题意可知,△ABC、△ADC是边长为1的正三角形,面积为$\frac{1}{2}×1×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,
设四面体A-BCD的内切球半径为r,则$\frac{1}{3}(1+\frac{\sqrt{3}}{2})r=\frac{1}{3}×\frac{1}{2}×1×1×\frac{\sqrt{2}}{2}$,得$r=\frac{2\sqrt{2}-\sqrt{6}}{2}$,命题(4)错误.
综上,正确的命题是(1)(2)(3).
故答案为:(1)(2)(3).
点评 本题考查命题的真假判断与应用,考查了空间想象能力和思维能力,是中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
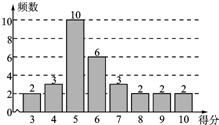 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为| A. | me=mo | B. | mo<me | C. | me<mo | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c≥$\sqrt{2}$-1 | B. | c≤$\sqrt{2}$-1 | C. | -1-$\sqrt{2}$≤c$≤\sqrt{2}-1$ | D. | $\sqrt{2}$-1≤c≤$\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③④ | B. | ①③④ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com