
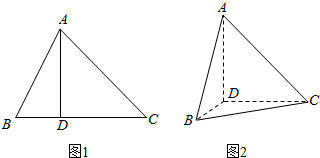
分析 (Ⅰ)证明:AD⊥平面BCD,即可证明平面ABD⊥平面BDC;
(Ⅱ)设BD=x,先利用线面垂直的判定定理证明AD即为三棱锥A-BCD的高,再将三棱锥的体积表示为x的函数,最后利用导数求函数的最大值即可.
解答 (Ⅰ)证明:在如图1所示的△ABC中,由折起前AD⊥BC知,折起后(如图2),AD⊥DC,AD⊥BD,
且BD∩DC=D,∴AD⊥平面BCD.
又AD?平面ABD,
∴面ABD⊥平面BDC. …(6分)
(Ⅱ)解:在△ABC中,设BD=x,则CD=3-x
∵∠ACB=45°,AD⊥BC,∴AD=CD=3-x
∵折起前AD⊥BC,∴折起后AD⊥BD,AD⊥CD,BD∩DC=D
∴AD⊥平面BCD
∴VA-BCD=$\frac{1}{3}$×AD×S△BCD=$\frac{1}{3}$×(3-x)×$\frac{1}{2}$×x(3-x)=$\frac{1}{6}$(x3-6x2+9x)
设f(x)=$\frac{1}{6}$(x3-6x2+9x) x∈(0,3),
∵f′(x)=$\frac{1}{2}$(x-1)(x-3),∴f(x)在(0,1)上为增函数,在(1,3)上为减函数
∴当x=1时,函数f(x)取最大值
∴当BD=1时,三棱锥A-BCD的体积最大. …(12分)
点评 本题主要考查了面面垂直的判定,考查三棱锥A-BCD的体积的计算,考查折叠问题中的不变量,有一定的运算量,属中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
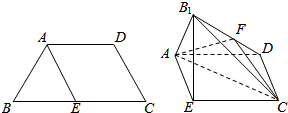 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
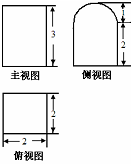
| A. | 20+2π | B. | 20+3π | C. | 24+3π | D. | 24+3π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com