
科目:高中数学 来源: 题型:
设同时满足条件:①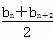 ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
(1) 若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;
(2) 判断(1)中的数列{Sn}是否为“特界” 数列,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(n)=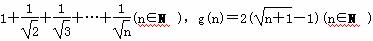 .
.
(1) 当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2) 由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线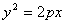
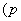 >
>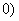 ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为 ( )
( )
A.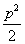 B.
B.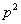 C.
C.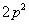 D.
D.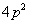
查看答案和解析>>
科目:高中数学 来源: 题型:
已知一个正四面体纸盒的俯视图如图所示,其中四边形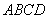 是边长为
是边长为 的正方形,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值为
的正方形,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值为
(A) (B)1
(B)1
(C)2 (D)

查看答案和解析>>
科目:高中数学 来源: 题型:
某花店每天以每枝10元的价格从农场购进若干支玫瑰花,并开始以每枝20元的价格出售,已知该花店的营业时间为8小时,若前7小时内所购进的玫瑰花没有售完,则花店对没卖出的玫瑰花以每枝5元的价格低价处理完毕(根据经验,1小时内完全能够把玫瑰花低价处理完毕,且处理完毕后,当天不再购进玫瑰花).该花店统计了100天内玫瑰花在每天的前7小时内的需求量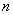 (单位:枝,
(单位:枝,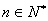 )(由于某种原因需求量频数表中的部分数据被污损而无法看清),制成如下表格(注:
)(由于某种原因需求量频数表中的部分数据被污损而无法看清),制成如下表格(注: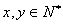 ;视频率为概率).
;视频率为概率).
| 前7小时内的需求量 | 14 | 15 | 16 | 17 |
| 频数 | 10 | 20 |
|
|
(Ⅰ)若花店一天购进16枝玫瑰花,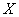 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求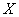 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)若花店每天购进16枝玫瑰花所获得的平均利润比每天购进17枝玫瑰花所获得的平均利润大,求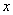 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设l是一条直线,α,β,γ是不同的平面,则在下列命题中,假命题是________.
①如果α⊥β,那 么α内一定存在直线平行于β
么α内一定存在直线平行于β
 ②如果α不垂
②如果α不垂 直于β,那么α内一定不存在直线垂直于β
直于β,那么α内一定不存在直线垂直于β
③如果α⊥γ,β⊥γ,α∩β= l,那么l⊥γ
l,那么l⊥γ
④如果α⊥β,l与α,β都相交,那么l与α,β所成的角互余
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com