
已知f(n)=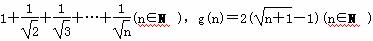 .
.
(1) 当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2) 由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
解:(1) 当n=1时,f(1)>g(1);
当n=2时,f(2)>g(2);
当n=3时,f(3)>g(3).
(2) 猜想:f(n)>g(n)(n∈N*),即 (n∈N*).
(n∈N*).
下面用数学归纳法证明:
①当n=1时,f(1)=1,g(1)=2(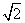 -1),f(1)>g(1).
-1),f(1)>g(1).
②假设当n=k时,猜想成立,即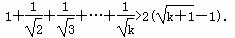
则当n=k+1时,f(k+1)=
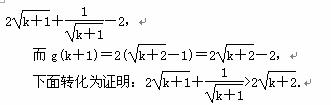
只要证:2(k+1)+1=2k+3>2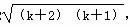 ,
,
需证:(2k+3)2>4(k+2)(k+1),
即证:4k2+12k+9>4k2+12k+8,此式显然成立.
所以,当n=k+1时猜想也成立.
综上可知:对n∈N*,猜想都成立,
即 (n∈N*)成立.
(n∈N*)成立.


科目:高中数学 来源: 题型:
用数学归纳法证明“12+22+32+…+n2= n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com