
分析 n个连续的正整数之积可表示为:S=k(k+1)(k+2)(k+3)…(k+n-1)=${A}_{k+n-1}^{n}$=${C}_{k+n-1}^{n}$•n!,命题得以证明.
解答 证明:不妨设这n个连续的正整数分别为:
k,k+1,k+2,k+3,…,k+n-1,(k,n∈N*),
它们的积记为S=k(k+1)(k+2)(k+3)…(k+n-1),
根据排列数公式,上式也可以写成:${A}_{k+n-1}^{n}$,
即S=${A}_{k+n-1}^{n}$,
再根据排列数和组合数之间的关系式,${A}_{m}^{n}$=${C}_{m}^{n}$•${A}_{n}^{n}$,
因此,${A}_{k+n-1}^{n}$=${C}_{k+n-1}^{n}$•${A}_{n}^{n}$,
所以,S=${A}_{k+n-1}^{n}$=${C}_{k+n-1}^{n}$•${A}_{n}^{n}$=${C}_{k+n-1}^{n}$•n!,
即k(k+1)(k+2)(k+3)…(k+n-1)=M•n!,
其中,M=${C}_{k+n-1}^{n}$∈N*,
所以,这连续n个正整数的乘积是n!的倍数.
点评 本题主要考查了整数中的整除问题,运用了构造法将问题转化为排列数与组合数的计算问题,属于中档题.


科目:高中数学 来源:2015-2016学年四川成都石室中学高一下期中数学试卷(解析版) 题型:选择题
已知等比数列 中,
中,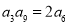 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则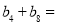 ( )
( )
A.2 B.4 C.8 D.16
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:选择题
已知函数 ,下列结论中不正确的是( )
,下列结论中不正确的是( )
A.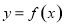 的图象关于点
的图象关于点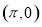 中心对称
中心对称
B.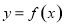 的图象关于直线
的图象关于直线 对称
对称
C.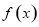 的最大值为
的最大值为
D.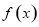 既是奇函数,又是周期函数
既是奇函数,又是周期函数
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:选择题
下列结论中,正确的是( )
A.“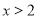 ”是“
”是“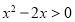 ”成立的必要条件
”成立的必要条件
B.命题“若 ,则
,则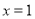 ”的逆否命题为假命题
”的逆否命题为假命题
C.命题“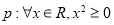 ”的否定形式为“
”的否定形式为“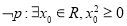 ”
”
D.已知向量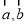 ,则“
,则“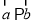 ”是“
”是“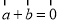 ” 的充要条件
” 的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{2}})$ | B. | $({-\sqrt{2},-1})∪({1,\sqrt{2}})$ | C. | $({-\sqrt{2},\sqrt{2}})$ | D. | $({-\sqrt{2},-1})∪({-1,1})∪({1,\sqrt{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com