
(3分)设函数f(x)=ax3﹣3x+1(x∈R),若对于任意的x∈[﹣1,1]都有f(x)≥0成立,则实数a的值为 .
4.
【解析】
试题分析:弦求出f′(x)=0时x的值,进而讨论函数的增减性得到f(x)的最小值,对于任意的x∈[﹣1,1]都有f(x)≥0成立,可转化为最小值大于等于0即可求出a的范围.
【解析】
由题意,f′(x)=3ax2﹣3,
当a≤0时3ax2﹣3<0,函数是减函数,f(0)=1,只需f(1)≥0即可,解得a≥2,与已知矛盾,
当a>0时,令f′(x)=3ax2﹣3=0解得x=±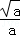 ,
,
①当x<﹣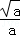 时,f′(x)>0,f(x)为递增函数,
时,f′(x)>0,f(x)为递增函数,
②当﹣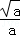 <x<
<x<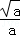 时,f′(x)<0,f(x)为递减函数,
时,f′(x)<0,f(x)为递减函数,
③当x>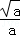 时,f(x)为递增函数.
时,f(x)为递增函数.
所以f( 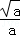 )≥0,且f(﹣1)≥0,且f(1)≥0即可
)≥0,且f(﹣1)≥0,且f(1)≥0即可
由f( 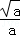 )≥0,即a•
)≥0,即a• ﹣3•
﹣3•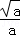 +1≥0,解得a≥4,
+1≥0,解得a≥4,
由f(﹣1)≥0,可得a≤4,
由f(1)≥0解得2≤a≤4,
综上a=4为所求.
故答案为:4.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:[同步]2014年苏教版必修三 2.3 总体特征数的估计练习卷(解析版) 题型:填空题
已知样本数据x1,x2,…xn的方差为4,则数据2x1+3,2x2+3,…2xn+3的标准差是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版必修一 1.2 子集、全集、补集练习卷(解析版) 题型:解答题
已知a∈R,b∈R,A={2,4,x2﹣5x+9},B={3,x2+ax+a},C={x2+(a+1)x﹣3,1}:求
(1)A={2,3,4}的x值;
(2)使2∈B,B?A,求a,x的值;
(3)使B=C的a,x的值.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷(解析版) 题型:填空题
某商品一件的成本为30元,在某段时间内,若以每件x元出售,可卖出(200﹣x)件,当每件商品的定价为 元时,利润最大.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.2导数的运算练习卷(解析版) 题型:解答题
已知P(﹣1,1),Q(2,4)是曲线y=x2上的两点,求与直线PQ平行且与曲线相切的切线方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.1 导数的概念练习卷(解析版) 题型:解答题
航天飞机升空后一段时间内,第t s时的高度h(t)=5t3+30t2+45t+4,其中h的单位为m,t的单位为s.
(1)h(0),h(1),h(2)分别表示什么?
(2)求第2s内的平均速度;
(3)求第2s末的瞬时速度.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.3 抛物线练习卷(解析版) 题型:选择题
动点到点(3,0)的距离比它到直线x=﹣2的距离大1,则动点的轨迹是( )
A.椭圆 B.双曲线 C.双曲线的一支 D.抛物线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com