
所已知数列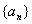 前项和
前项和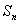 且
且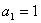 ,
,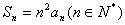
(1)试求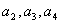
(2)猜想 的表达式,并用数学归纳法证明猜想.
的表达式,并用数学归纳法证明猜想.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
如果函数f(x)在区间D上是“凸函数”,则对于区间D内任意的x1,x2,…,xn,有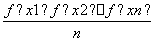 ≤f
≤f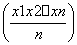 成立.已知函数y=sin x在区间上是“凸函数”,则在△ABC中,sin A+sin B+sin C的最大值是
成立.已知函数y=sin x在区间上是“凸函数”,则在△ABC中,sin A+sin B+sin C的最大值是
查看答案和解析>>
科目:高中数学 来源: 题型:
为了响应学校“学科文化节”活动,数学组举办了一场数学知识竞赛,共分为甲、乙两组.其中甲组得满分的有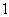 个女生和
个女生和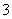 个男生,乙组得满分的有
个男生,乙组得满分的有 个女生和
个女生和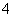 个男生.现从得满分的学生中,每组各任选
个男生.现从得满分的学生中,每组各任选 个学生,作为数学组的活动代言人.
个学生,作为数学组的活动代言人.
(1)求选出的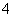 个学生中恰有
个学生中恰有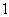 个女生的概率;
个女生的概率;
(2)设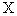 为选出的
为选出的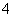 个学生中女生的人数,求
个学生中女生的人数,求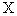 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆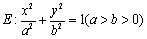 过点
过点 ,离心率为
,离心率为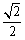 .
.
(1)若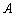 是椭圆
是椭圆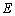 的上顶点,
的上顶点,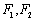 分别是左右焦点,直线
分别是左右焦点,直线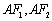 分别交椭圆于
分别交椭圆于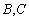 ,直线
,直线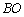 交
交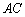 于D,求证
于D,求证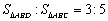 ;
;
(2)若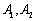 分别是椭圆
分别是椭圆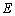 的左右顶点,动点
的左右顶点,动点 满足
满足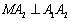 ,且
,且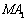 交椭圆
交椭圆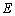 于点
于点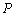 .
.
求证: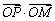 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com