
分析 由$\overrightarrow{PA}=\overrightarrow{PC}+\overrightarrow{CA}$,$\overrightarrow{PB}=\overrightarrow{PC}+\overrightarrow{CB}$,$\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{0},\overrightarrow{CA}•C\overrightarrow{B}=-1$
得$\overrightarrow{PA}•\overrightarrow{PB}$=($\overrightarrow{PC}+\overrightarrow{CA}$)•($\overrightarrow{PC}+\overrightarrow{CB})$=${\overrightarrow{PC}}^{2}+\overrightarrow{PC}(\overrightarrow{CB}+\overrightarrow{CA})+\overrightarrow{CA}•\overrightarrow{CB}$
=${\overrightarrow{PC}}^{2}-1$=x2+(y-1)2-1=x2+y2-2y=-3y2-2y+4
再结合y的范围即可求出结论
解答 解:设P(x,y),
∵$\overrightarrow{PA}=\overrightarrow{PC}+\overrightarrow{CA}$,$\overrightarrow{PB}=\overrightarrow{PC}+\overrightarrow{CB}$,$\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{0},\overrightarrow{CA}•C\overrightarrow{B}=-1$
∴$\overrightarrow{PA}•\overrightarrow{PB}$=($\overrightarrow{PC}+\overrightarrow{CA}$)•($\overrightarrow{PC}+\overrightarrow{CB})$=${\overrightarrow{PC}}^{2}+\overrightarrow{PC}(\overrightarrow{CB}+\overrightarrow{CA})+\overrightarrow{CA}•\overrightarrow{CB}$
=${\overrightarrow{PC}}^{2}-1$=x2+(y-1)2-1=x2+y2-2y=-3y2-2y+4
∵y∈[-1,1],∴-3y2-2y+4$∈[-1,\frac{13}{3}]$,
∴$\overrightarrow{PA}•\overrightarrow{PB}$的取值范围是:[-1,$\frac{13}{3}$].
故答案为:[-1,$\frac{13}{3}$]
点评 本题主要考查椭圆的基本性质,向量数量积的基本运算技巧,选好基底是解决向量问题的基本技巧之一,及二次函数的值域问题,属于中档题,


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{37}}}{2}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{37}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 3 | B. | $\frac{17}{7}$ | C. | $\frac{7}{3}$ | D. | $\frac{3}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧(¬q) | B. | (¬p)∧q | C. | p∧q | D. | (¬p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
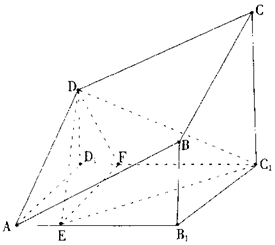 如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.
如图BB1,CC1,DD1均垂直于正方形AB1C1D1所在平面A、B、C、D四点共面.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com