
分析 (Ⅰ)f′(x)=x2-(a+1)x+a,令f′(x)=0得x1=1,x2=a,由题意函数f(x)在区间(0,2)无最值,知f(x)在(0,2)上要么有两个极值点或者没有极值点,即可求a的取值范围;
(Ⅱ)不妨设2≤x1<x2≤3,由(Ⅰ)知:当a≥3时,f(x)在区间[2,3]上恒单调递减,有|f(x1)-f(x2)|=f(x1)-f(x2),分类讨论,构造函数,即可求实数a的取值范围.
解答 解:(Ⅰ)f′(x)=x2-(a+1)x+a,令f′(x)=0得x1=1,x2=a,…(1分)
依题意函数f(x)在区间(0,2)无最值,
知f(x)在(0,2)上要么有两个极值点或者没有极值点,
知1≤a<2,…(3分)$f(1)=\frac{1}{3}-\frac{a+1}{2}+a-1=\frac{a}{2}-\frac{7}{6}$,$f(a)=\frac{1}{3}{a^3}-\frac{a+1}{2}{a^2}+{a^2}-1$,f(0)=-1,$f(2)=\frac{8}{3}-2(a+1)+2a-1=-\frac{1}{3}$,
(i)若a=1,函数f(x)在区间(0,2)上恒单调递增,显然符合题意;…(4分)
(ii)若1<a<2时,有$\left\{{\begin{array}{l}{f(1)<f(2)}\\{f(a)>f(0)}\end{array}}\right.$,
即$\left\{{\begin{array}{l}{\frac{a}{2}-\frac{7}{6}<-\frac{1}{3}}\\{\frac{1}{3}{a^3}-\frac{a+1}{2}{a^2}+{a^2}-1>-1}\end{array}}\right.$,$\left\{{\begin{array}{l}{a<\frac{5}{3}}\\{a<3}\end{array}}\right.$,
得$1<a<\frac{5}{3}$;
综上有$1≤a<\frac{5}{3}$.…(6分)
(Ⅱ)不妨设2≤x1<x2≤3,
由(Ⅰ)知:当a≥3时,f(x)在区间[2,3]上恒单调递减,
有|f(x1)-f(x2)|=f(x1)-f(x2),…(7分)
(i)若3≤a≤4时,$g(x)=\frac{1}{2}(a-4){x^2}$在区间[2,3]上恒单调递减,|g(x1)-g(x2)|=g(x1)-g(x2),
则|f(x1)-f(x2)|>|g(x1)-g(x2)|等价于f(x1)-g(x1)>f(x2)-g(x2),
令函数F(x)=f(x)-g(x),
由F(x1)>F(x2)知F(x)在区间[2,3]上单调递减,F′(x)=x2-(a+1)x+a-(a-4)x=x2-(2a-3)x+a,
当a≥3时,x2-(2a-3)x+a≤0,
即$\left\{\begin{array}{l}{2^2}-2×(2a-3)+a≤0\\{3^2}-3×(2a-3)+a≤0\end{array}\right.$,求得$\frac{18}{5}≤a≤4$;…(10分)
(ii)若a>4时,$g(x)=\frac{1}{2}(a-4){x^2}$单调递增,|g(x1)-g(x2)|=g(x2)-g(x1),
则|f(x1)-f(x2)|>|g(x1)-g(x2)|等价于f(x1)+g(x1)>f(x2)+g(x2),
令函数G(x)=f(x)+g(x),
由G(x1)>G(x2)知G(x)在区间[2,3]上单调递减,
有G′(x)=x2-(a+1)x+a+(a-4)x=x2-5x+a≤0,
故当2≤x≤3时,x2-5x+a≤0,
即$\left\{\begin{array}{l}4-10+a≤0\\ 9-15+a≤0\end{array}\right.$,求得4<a≤6,
由(i)(ii)得$\frac{18}{5}≤a≤6$. …(12分)
点评 本题考查导数知识的综合运用,考查函数的单调性,考查恒成立问题,考查分类讨论的数学思想,有难度.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
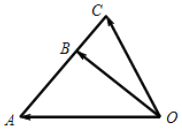
| A. | $\overrightarrow c=\frac{3}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$ | B. | $\overrightarrow c=2\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow c=2\overrightarrow a-\overrightarrow b$ | D. | $\overrightarrow c=\frac{3}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
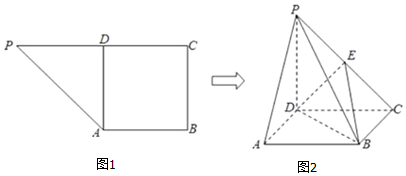
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com