
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
分析 以CA为x轴,CB为y轴建立直角坐标系,设P(cosθ,sinθ),再代入计算即可.
解答 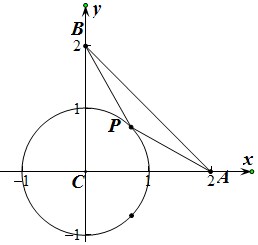 解:以CA为x轴,CB为y轴建立直角坐标系,设P(cosθ,sinθ),
解:以CA为x轴,CB为y轴建立直角坐标系,设P(cosθ,sinθ),
∵△ABC是底边边长为2$\sqrt{2}$的等腰直角三角形,
∴A(2,0),B(0,2),
∴$\overrightarrow{AP}$=(cosθ-2,sinθ),$\overrightarrow{PB}$=(-cosθ,2-sinθ),
∴$\overrightarrow{AP}$•$\overrightarrow{PB}$=cos2θ-2cosθ+2sinθ-sin2θ=2$\sqrt{2}$sin(θ-$\frac{π}{4}$)-1,
∵-1≤sin(θ-$\frac{π}{4}$)≤1,
∴-2$\sqrt{2}$+1≤2$\sqrt{2}$sin(θ-$\frac{π}{4}$)-1≤2$\sqrt{2}$+1,
∵m≤$\overrightarrow{AP}$•$\overrightarrow{PB}$≤n,
∴m=1-2$\sqrt{2}$,n=1+2$\sqrt{2}$,
∴n-m=4$\sqrt{2}$,
故选:A
点评 本题的关键在建立坐标系,然后用三角代换表示各点的坐标,这样使得问题容易表达并易于求解,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{9}{2}$π+24 | B. | $\frac{9}{2}$π+30 | C. | 9π+54 | D. | 36π+30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
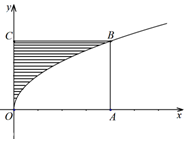 如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )
如图,长方形OABC中,O为坐标原点,点C在y轴上,A(4,0),曲线y2=ax(a>0)经过点B,现将一质点随机投入长方形OABC中,若质点落在图中阴影区域的概率是( )| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-$\frac{3}{2}$)2+y2=25 | B. | (x+$\frac{3}{2}$)2+y2=$\frac{1}{4}$ | C. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | D. | x2+(y-$\frac{3}{2}$)2=$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1,DF交于点E,且AB1⊥DF,则下列结论中不正确的是( )| A. | CE与BC1异面且垂直 | B. | AB1⊥C1F | ||
| C. | △C1DF是直角三角形 | D. | DF的长为$\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com