
分析 (1)由题意求得焦点及准线方程,即可求得圆心,利用点到直线的距离公式,即可求得半径,即可求得圆的方程;
(2)方法一:设直线AB方程为y=k(x-1),代入椭圆方程,利用韦达定理,求得直线BA′的方程为,当y=0,求得x=-1,则直线BA′过定点(-1,0);
方法二:设直线AB方程为y=k(x-1),代入椭圆方程,利用韦达定理求得kA′M-kBM=0,则kA′M=kBM=0,A′、B、M三点共线,则直线BA′过定点(-1,0);
方法三:设直线AB的方程:x=my+1,求得直线BA′的方程为,利用韦达定理可得y=$\frac{4}{{{y_2}-{y_1}}}({x+1})$,则直线BA′过定点(-1,0).
解答 解:(1)抛物线E:y2=4x的准线l的方程为:x=-1,焦点坐标为F(1,0),
设所求圆的圆心C(a,b),半径为r,∵圆C过O,F,
∴$a=\frac{1}{2}$,∵圆C与直线l:x=-1相切,
∴$r=\frac{1}{2}-({-1})=\frac{3}{2}$.
由$r=|{CO}|=\sqrt{{{({\frac{1}{2}})}^2}+{b^2}}=\frac{3}{2}$,得$b=±\sqrt{2}$.
∴过O,F,且与直线l相切的圆的方程为${({x-\frac{1}{2}})^2}+{({y±\sqrt{2}})^2}=\frac{9}{4}$;
(2)证明:解法一:依题意知直线AB的斜率存在,设直线AB方程为y=k(x-1),A(x1,y1),B(x2,y2),(x1≠x2),A′(x1,-y1),
联立$\left\{\begin{array}{l}y=k({x-1})\\{y^2}=4x\end{array}\right.$,消去y得k2x2-(2k2+4)x+k2=0.
∴${x_1}+{x_2}=\frac{{2{k^2}+4}}{k^2}$,x1•x2=1.
∵直线BA′的方程为$y-{y_2}=\frac{{{y_2}+{y_1}}}{{{x_2}-{x_1}}}({x-{x_2}})$,
∴令y=0,得$x=\frac{{{x_2}{y_1}+{x_1}{y_2}}}{{{y_1}+{y_2}}}=\frac{{{x_2}k({{x_2}-1})+{x_1}k({{x_2}-1})}}{{k({{x_1}-1})+k({{x_2}-1})}}=\frac{{2{x_1}{x_2}-({{x_1}+{x_2}})}}{{-2+({{x_1}+{x_2}})}}=-1$.
直线BA′过定点(-1,0),
解法二:直线BA′过定点M(-1,0).
证明:依题意知直线AB的斜率存在,设直线AB方程为y=k(x-1),A(x1,y1),B(x2,y2),(x1≠x2),A′(x1,-y1),
联立$\left\{\begin{array}{l}y=k({x-1})\\{y^2}=4x\end{array}\right.$,消去y得k2x2-(2k2+4)x+k2=0,
∴${x_1}+{x_2}=\frac{{2{k^2}+4}}{k^2}$,x1•x2=1.
∵${k_{A′M}}-{k_{BM}}=\frac{{-{y_1}}}{{{x_1}+1}}-\frac{y_2}{{{x_2}+1}}=-\frac{{{x_2}{y_1}+{x_1}{y_2}+{y_1}+{y_2}}}{{({{x_1}+1})({{x_2}+1})}}$,
∵x2y1+x1y2+y1+y2=k(x1-1)x2+k(x2-1)x1+k(x1+x2-2)=2kx1x2-2k=2k•1-2k=0.
∴kA′M-kBM=0,即kA′M=kBM=0,A′、B、M三点共线,
∴直线BA′过定点(-1,0).
解法三:设直线AB的方程:x=my+1,A(x1,y1),B(x2,y2),则A′(x1,-y1).
由$\left\{\begin{array}{l}y=k({x-1})\\{y^2}=4x\end{array}\right.$得,y2-4my-4=0.
∴y1+y2=4m,y1•y2=-4.
∵${k_{BA′}}=\frac{{{y_2}+{y_1}}}{{{x_2}-{x_1}}}=\frac{{{y_2}+{y_1}}}{{\frac{{{y_2}^2}}{4}-\frac{{{y_1}^2}}{4}}}=\frac{4}{{{y_2}-{y_1}}}$,
∴直线BA′的方程为$y-{y_2}=\frac{{{y_2}+{y_1}}}{{{x_2}-{x_1}}}({x-{x_2}})$.
∴$y=\frac{4}{{{y_2}-{y_1}}}({x-{x_2}})+{y_2}=\frac{4}{{{y_2}-{y_1}}}x+{y_2}-\frac{{4{x_2}}}{{{y_2}-{y_1}}}=\frac{4}{{{y_2}-{y_1}}}x+\frac{{{y_2}^2-{y_1}{y_2}-4{x_2}}}{{{y_2}-{y_1}}}=\frac{4}{{{y_2}-{y_1}}}x+\frac{4}{{{y_2}-{y_1}}}$=$\frac{4}{{{y_2}-{y_1}}}({x+1})$.
∴直线BA′过定点(-1,0).
点评 本题考查抛物线的简单性质,直线与抛物线的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∨q | C. | (¬p)∧q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
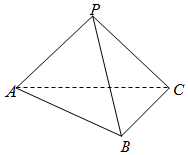 如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.
如图,在三棱锥P-ABC中,平面ABC⊥平面APC,AB=BC=AP=PC=$\sqrt{2}$,∠ABC=∠APC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
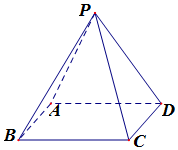 如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD⊥底面ABCD,PA⊥PC;
如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD⊥底面ABCD,PA⊥PC;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com