
分析 (I)曲线C1的参数方程为$\left\{\begin{array}{l}x=2cosφ\\ y=2+2sinφ\end{array}$(φ为参数),消去参数可得普通方程.曲线C2的极坐标方程为ρ=4$\sqrt{3}$cosθ,即ρ2=4$\sqrt{3}$ρcosθ,利用互化公式可得直角坐标方程,联立解出即可得出.
(II)曲线C3的参数方程为$\left\{{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}}\right.$(0≤α<π,t为参数,且t≠0),$α=\frac{π}{2}$时,不满足|PQ|=8,舍去.
$α≠\frac{π}{2}$时,消去参数化为普通方程:y=xtanα,设k=tanα,即直线l的方程为:y=kx,分别与曲线C1,C2的方程联立解出交点P,Q的坐标,利用两点之间的距离公式即可得出.
解答 解:(I)曲线C1的参数方程为$\left\{\begin{array}{l}x=2cosφ\\ y=2+2sinφ\end{array}$(φ为参数),
消去参数可得:x2+(y-2)2=4.
曲线C2的极坐标方程为ρ=4$\sqrt{3}$cosθ,即ρ2=4$\sqrt{3}$ρcosθ,
化为直角坐标方程:x2+y2=4$\sqrt{3}$x.
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-4y=0}\\{{x}^{2}+{y}^{2}=4\sqrt{3}x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=3}\end{array}\right.$,
∴C1与C2交点的直角坐标分别为:(0,0);$(\sqrt{3},3)$.
(II)曲线C3的参数方程为$\left\{{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}}\right.$(0≤α<π,t为参数,且t≠0),
$α=\frac{π}{2}$时,可得$\left\{\begin{array}{l}{x=0}\\{y=t}\end{array}\right.$,代入方程:x2+(y-2)2=4,解得t=0,t=4.
代入:x2+y2=4$\sqrt{3}$x,解得t=0,不满足|PQ|=8,舍去.
$α≠\frac{π}{2}$时,消去参数化为普通方程:y=xtanα,设k=tanα.
联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+{y}^{2}-4y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{4k}{1+{k}^{2}}}\\{y=\frac{4{k}^{2}}{1+{k}^{2}}}\end{array}\right.$,
可得P(0,0),或P$(\frac{4k}{1+{k}^{2}},\frac{4{k}^{2}}{1+{k}^{2}})$.
联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+{y}^{2}=4\sqrt{3}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{4\sqrt{3}}{1+{k}^{2}}}\\{y=\frac{4\sqrt{3}k}{1+{k}^{2}}}\end{array}\right.$,
可得Q(0,0),或Q$(\frac{4\sqrt{3}}{1+{k}^{2}},\frac{4\sqrt{3}k}{1+{k}^{2}})$.
∵|PQ|=8,∴只能取P$(\frac{4k}{1+{k}^{2}},\frac{4{k}^{2}}{1+{k}^{2}})$,Q$(\frac{4\sqrt{3}}{1+{k}^{2}},\frac{4\sqrt{3}k}{1+{k}^{2}})$.
∴$(\frac{4k-4\sqrt{3}}{1+{k}^{2}})^{2}$+$(\frac{4{k}^{2}-4\sqrt{3}k}{1+{k}^{2}})^{2}$=82,
化为:$(\sqrt{3}k+1)^{2}$=0,解得k=-$\frac{\sqrt{3}}{3}$,
∴tanα=-$\frac{\sqrt{3}}{3}$,又0≤α<π,解得α=$\frac{5π}{6}$.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、直线与圆的交点、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
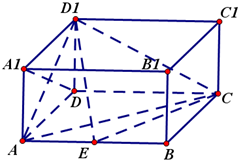 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
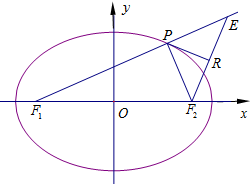 已知F1,F2分别为椭圆的左、右两个焦点,椭圆的离心率为$\frac{\sqrt{6}}{3}$,短轴的一个端点到一个焦点的距离为$\sqrt{3}$.设点P是椭圆上的动点,过点F2作∠F1PF2的外角平分线PR的垂线,交F1P的延长线于E,垂足为R.
已知F1,F2分别为椭圆的左、右两个焦点,椭圆的离心率为$\frac{\sqrt{6}}{3}$,短轴的一个端点到一个焦点的距离为$\sqrt{3}$.设点P是椭圆上的动点,过点F2作∠F1PF2的外角平分线PR的垂线,交F1P的延长线于E,垂足为R.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com