
| A. | (0,1]∪[2$\sqrt{3}$,+∞) | B. | (0,1]∪[3,+∞) | C. | (0,$\sqrt{2}$)∪[2$\sqrt{3}$,+∞) | D. | (0,$\sqrt{2}$]∪[3,+∞) |
分析 根据题意,由二次函数的性质分析可得:y=(mx-1)2 为二次函数,在区间(0,$\frac{1}{m}$)为减函数,($\frac{1}{m}$,+∞)为增函数,分2种情况讨论:①、当0<m≤1时,有$\frac{1}{m}$≥1,②、当m>1时,有$\frac{1}{m}$<1,结合图象分析两个函数的单调性与值域,可得m的取值范围,综合可得答案.
解答 解:根据题意,由于m为正数,y=(mx-1)2 为二次函数,在区间(0,$\frac{1}{m}$)为减函数,($\frac{1}{m}$,+∞)为增函数,
函数y=$\sqrt{x}$+m为增函数,
分2种情况讨论:
①、当0<m≤1时,有$\frac{1}{m}$≥1,
在区间[0,1]上,y=(mx-1)2 为减函数,且其值域为[(m-1)2,1],
函数y=$\sqrt{x}$+m为增函数,其值域为[m,1+m],
此时两个函数的图象有1个交点,符合题意;
②、当m>1时,有$\frac{1}{m}$<1,
y=(mx-1)2 在区间(0,$\frac{1}{m}$)为减函数,($\frac{1}{m}$,1)为增函数,
函数y=$\sqrt{x}$+m为增函数,其值域为[m,1+m],
若两个函数的图象有1个交点,则有(m-1)2≥1+m,
解可得m≤0或m≥3,
又由m为正数,则m≥3;
综合可得:m的取值范围是(0,1]∪[3,+∞);
故选:B.
点评 本题考查函数图象的交点问题,涉及函数单调性的应用,关键是确定实数m的分类讨论.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 160 | B. | 163 | C. | 166 | D. | 170 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
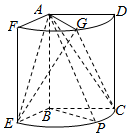 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com