练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．在△ABC中，若已知AC=10，BC=15和A=60°，则sinB=$\frac{\sqrt{3}}{3}$．

    分析 由已知利用正弦定理即可计算得解．

    解答 解：在△ABC中，∵AC=10，BC=15和A=60°，
    ∴由正弦定理可得：sinB=$\frac{AC•sinA}{BC}$=$\frac{10×\frac{\sqrt{3}}{2}}{15}$=$\frac{\sqrt{3}}{3}$．
    故答案为：$\frac{\sqrt{3}}{3}$．

    点评 本题主要考查了正弦定理在解三角形中的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．已知圆${C_1}：{x^2}+{y^2}-2x+4y-4=0$，圆${C_2}：{x^2}+{y^2}+2x+2y-2=0$，圆${C_3}：{x^2}+{y^2}-2x-2y-\frac{14}{5}=0$，则圆C1与圆C2的公共弦所在的直线被圆C3所截得的弦长为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数f（x）=x2-1的单调递减区间为（　　）
    A．[0，+∞）B．（-∞，0]C．[-1，+∞）D．（-∞，-1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知tanα=2，求1-3sinαcosα+3cos2α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

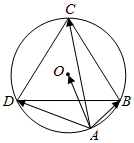    7．如图，设正△BCD的外接圆O的半径为R（$\frac{1}{2}$＜R＜$\frac{\sqrt{3}}{3}$），点A在BD下方的圆弧上，则（$\overrightarrow{AO}$-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$-$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$）•$\overrightarrow{AC}$的最小值为-$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在△ABC中，若b2-c2-a2=-ac，则B等于（　　）
    A．120°B．30°或150°C．45°D．60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知函数f（x）=2sinωxcosωx-2$\sqrt{3}$cos2ωx相邻对称轴之间的距离为$\frac{π}{2}$，则下列结论中错误的是（　　）
    A．f（x）在区间（0，$\frac{π}{4}$）上单调递增
    B．f（x）的一个对称中心为（$\frac{π}{6}$，-$\sqrt{3}$）
    C．当x∈[0，$\frac{π}{2}$]时，f（x）的值域为[-2$\sqrt{3}$，0]
    D．将f（x）的纵坐标不变，横坐标缩短为原来的$\frac{1}{2}$，再向左平移$\frac{π}{6}$个单位后得到y=2sin（4x+$\frac{π}{3}$）-$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知等比数列{an}的公比q=$\frac{1}{3}$，并且a1+a3+a5+…+a99=60，那么a1+a2+a3+…+a100等于$\frac{60（{3}^{100}-1）}{（{3}^{66}-1）•{3}^{34}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设等差数列{an}的前n项和为Sn，若a3=3，Sm=19，Sm+5=14，则m的值为9．

    查看答案和解析>>

    同步练习册答案