练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知矩形ABCD的边AB=1，BC=a，PA⊥平面ABCD，PA=1，问

     
    BC边上是否存在点Q，使得PQ⊥QD，并说明理由.


    解：连接AQ，因PA⊥平面ABCD，所以PQ⊥QDAQ⊥QD，即以AD为直经的圆与BC有交点．

    当AD=BC=aAB=1,即a1时，在BC边上存在点Q，使得PQ⊥QD；．．．．．．．．．7分

    当0<a<1时，在BC边上不存在点Q，使得PQ⊥QD．．．．．．．．．．．．．．．．．．．．．．12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知，且．

    (Ⅰ) 求的值；

    (Ⅱ) 求的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    P(x，y)在圆C：(x－1)2＋(y－1)2＝1上移动，试求x2＋y2的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列关于互不相同的直线l、m、n和平面α、β、γ的三个命题：

    ①若l与m为异面直线，l⊂α，m⊂β，则α∥β； ②若α∥β，l⊂α，m⊂β，则l∥m；

    ③若α∩β＝l，β∩γ＝m，γ∩α＝n，l∥γ，则m∥n.

    其中真命题的个数为                   (　　)

    A.3　　　　    B.2　　　　    C.1　　　　    D.0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    α、β是两个不同的平面，m、n是平面α、β外的两条不同直线，给出四个结论：

    ①m⊥n;     ②α⊥β;     ③n⊥β;        ④m⊥α.

    以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题______

    查看答案和解析>>

    科目：高中数学 来源： 题型：


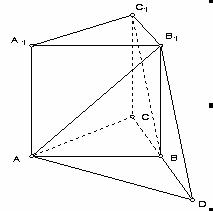
    如图，正三棱柱ABC—A1B1C1的底面边长的3，侧棱AA1=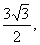D是CB延长线上一点，且BD=BC.

       （Ⅰ）求证：直线BC1//平面AB1D；

       （Ⅱ）求二面角B1—AD—B的大小；

       （Ⅲ）求三棱锥C1—ABB1的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有4名教师参加说课比赛，共有4道备选题目，若每位教师从中有放回地随机选出一道题目进行说课，其中恰有一道题目没有被这4位教师选中的情况有(　　)

    A．288种         B．144种            C．72种             D．36种

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的导数是：（      ）

    A．                B．

    C．                       D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    三个平面最多把空间分割成                 个部分。

    查看答案和解析>>

    同步练习册答案