Question

17．已知函数f（x）为偶函数，当x＜0时，f（x）=ln（-x）-ax．若直线y=x与曲线y=f（x）至少有两个交点，则实数a的取值范围是（　　）

• A． $[{-1-\frac{1}{e}，1-\frac{1}{e}}]$
• B． $（{-1-\frac{1}{e}，-1}）∪\left\{{1-\frac{1}{e}}\right\}$
• C． $（{1-\frac{1}{e}，+∞}）$
• D． $（{-1-\frac{1}{e}，-1}）∪[{1-\frac{1}{e}，+∞}）$

Answer 1

分析 由函数是偶函数求出函数解析式，把直线y=x与曲线y=f（x）至少有两个交点转化为方程f（x）=x至少有两个根．令g（x）=f（x）-x=$\left\{\begin{array}{l}{ln（-x）-ax-x，x＜0}\\{lnx+ax-x，x＞0}\end{array}\right.$．然后对x＜0和x＞0分类求解g（x）的零点个数，然后运用交集思想得答案．

解答 解：设x＞0，则-x＜0，
∵f（x）为偶函数，且当x＜0时，f（x）=ln（-x）-ax，
∴当x＞0时，f（x）=f（-x）=lnx+ax．
∴f（x）=$\left\{\begin{array}{l}{ln（-x）-ax，x＜0}\\{lnx+ax，x＞0}\end{array}\right.$．
若直线y=x与曲线y=f（x）至少有两个交点，即方程f（x）=x至少有两个根．
令g（x）=f（x）-x=$\left\{\begin{array}{l}{ln（-x）-ax-x，x＜0}\\{lnx+ax-x，x＞0}\end{array}\right.$．
下面研究：
当x＜0时，函数g（x）=ln（-x）-ax-x零点情况：
由g（x）=ln（-x）-ax-x=0，得ln（-x）=（a+1）x．
作出y=ln（-x）的图象如图：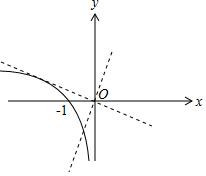

若a+1≥0，即a≥-1，则y=ln（-x）与y=（a+1）x有1个交点，
若a+1＜0，即a＜-1，设直线y=（a+1）x与y=ln（-x）的切点为（x₀，ln（-x₀）），
则切线方程为y-ln（-x₀）=$\frac{1}{{x}_{0}}$（x-x₀），代入原点（0，0），可得ln（-x₀）=1，x₀=-e．
则切点为（-e，1），切线斜率为-$\frac{1}{e}$，要使直线y=（a+1）x与y=ln（-x）有交点，则a+1$≥-\frac{1}{e}$，即a$≥-1-\frac{1}{e}$；
当x＞0时，函数g（x）=lnx+ax-x零点情况：
由g（x）=lnx+ax-x=0，得lnx=（-a+1）x．
作出y=lnx的图象如图：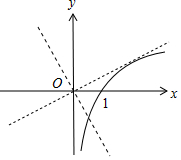

若-a+1≤0，即a≥1，则y=lnx与y=（-a+1）x有1个交点，
若-a+1＞0，即a＜1，设直线y=（-a+1）x与y=lnx的切点为（x₀，lnx₀），
则切线方程为y-lnx₀=$\frac{1}{{x}_{0}}$（x-x₀），代入原点（0，0），可得lnx₀=1，x₀=e．
则切点为（e，1），切线斜率为$\frac{1}{e}$，要使直线y=（-a+1）x与y=lnx有交点，则-a+1$≤\frac{1}{e}$，即$a≥1-\frac{1}{e}$．
综上，满足直线y=x与曲线y=f（x）至少有两个交点，则实数a的取值范围是$（{-1-\frac{1}{e}，-1}）∪[{1-\frac{1}{e}，+∞}）$．
故选：D．

点评 本题考查根的存在性及根的个数判断，考查数学转化思想方法与分类讨论的数学思想方法，训练了利用导数研究过曲线上某点处的切线方程，是压轴题．