
分析 (Ⅰ)f(1)=1,f($\frac{1}{2}$)=$\frac{3}{4}$,求出函数的解析式f(x)=$\frac{3x}{2x+1}$,然后求解x2,x3.
(Ⅱ)通过xn+1=f(xn)=$\frac{3{x}_{n}}{2{x}_{n}+1}$,推出数列{$\frac{1}{{x}_{n}}-1$}是以$-\frac{1}{3}$为首项,$\frac{1}{3}$为公比的等比数列,然后求解数列{xn}的通项公式.
(Ⅲ)xn=$\frac{{3}^{n}}{{3}^{n}-1}$.可得$\frac{{x}_{n}}{{3}^{n}}=\frac{1}{{3}^{n}-1}$,推出$\frac{{x}_{k}}{{3}^{k}}$=$\frac{1}{{3}^{k}-1}$≤$\frac{1}{2•{3}^{k-1}}(k∈{N}^{+})$,利用等比数列求和化简证明即可.
解答 解:(Ⅰ)函数f(x)=$\frac{3x}{ax+b}$,f(1)=1,f($\frac{1}{2}$)=$\frac{3}{4}$,可得:$\left\{\begin{array}{l}{a+b=3}\\{a+2b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
f(x)=$\frac{3x}{2x+1}$,x2=f(x1)=f($\frac{3}{2}$)=$\frac{9}{8}$,x3=f(x2)=f($\frac{9}{8}$)=$\frac{27}{26}$.
(Ⅱ)xn+1=f(xn)=$\frac{3{x}_{n}}{2{x}_{n}+1}$,$\frac{1}{{x}_{n+1}}=\frac{2{x}_{n}+1}{3{x}_{n}}$=$\frac{1}{3}•\frac{1}{{x}_{n}}+\frac{2}{3}$,
$\frac{1}{{x}_{n+1}}-1=\frac{1}{3}(\frac{1}{{x}_{n}}-1)$,
∴数列{$\frac{1}{{x}_{n}}-1$}是以$-\frac{1}{3}$为首项,$\frac{1}{3}$为公比的等比数列,
所以$\frac{1}{{x}_{n}}-1=-\frac{1}{{3}^{n}}$,
数列{xn}的通项公式.xn=$\frac{{3}^{n}}{{3}^{n}-1}$.
(Ⅲ)证明:xn=$\frac{{3}^{n}}{{3}^{n}-1}$.可得$\frac{{x}_{n}}{{3}^{n}}=\frac{1}{{3}^{n}-1}$,3n-1=3•3n-1-1=2•3n-1+3n-1-1≥2•3n-1,
∴$\frac{{x}_{k}}{{3}^{k}}$=$\frac{1}{{3}^{k}-1}$≤$\frac{1}{2•{3}^{k-1}}(k∈{N}^{+})$,
∴$\sum_{k=1}^{n}\frac{{x}_{k}}{{3}^{k}}$≤$\frac{1}{2}(1+\frac{1}{3}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{n-1}})$=$\frac{1}{2}•\frac{1-\frac{1}{{3}^{n}}}{1-\frac{1}{3}}$=$\frac{3}{4}•(1-\frac{1}{{3}^{n}})$<$\frac{3}{4}$.
点评 本题考查数列与函数的综合应用,数列求和,数列递推关系式的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
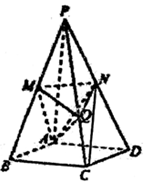 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分别为PB,PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 22 | 6 | 28 |
| 女生 | 10 | 10 | 20 |
| 合计 | 32 | 16 | 48 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{8}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com