
(本小题满分14分)已知函数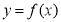 ,
,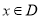 ,设曲线
,设曲线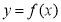 在点
在点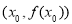 处的切线方程为
处的切线方程为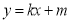 . 如果对任意的
. 如果对任意的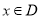 ,均有:
,均有:
①当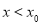 时,
时,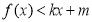 ;
;
②当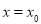 时,
时, ;
;
③当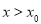 时,
时,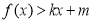 ,
,
则称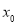 为函数
为函数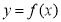 的一个“? -点”.
的一个“? -点”.
(1)判断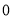 是否是下列函数的“? -点”:
是否是下列函数的“? -点”:
①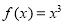 ; ②
; ②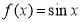 .(只需写出结论)
.(只需写出结论)
(2)设函数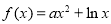 .
.
(ⅰ)若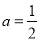 ,证明:
,证明: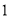 是函数
是函数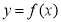 的一个“? -点”;
的一个“? -点”;
(ⅱ)若函数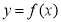 存在“? -点”,直接写出
存在“? -点”,直接写出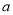 的取值范围.
的取值范围.
(1)①0是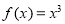 的“? -点”; ②0不是
的“? -点”; ②0不是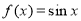 的“? -点”.(2)(ⅰ)详见解析(ⅱ)
的“? -点”.(2)(ⅰ)详见解析(ⅱ)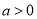
【解析】
试题分析:(1)分别求两个函数的导数,及其在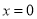 处的切线方程.然后判断
处的切线方程.然后判断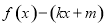 在
在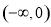 ,
,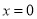 和
和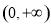 的符号.(2)(ⅰ)先求导,再求在
的符号.(2)(ⅰ)先求导,再求在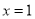 处的切线的方程为
处的切线的方程为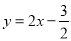 .令
.令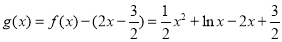 .在求导,讨论导数的符号可得函数
.在求导,讨论导数的符号可得函数 的单调性.根据其单调性判断函数
的单调性.根据其单调性判断函数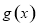 在
在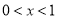 时,
时, 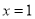 时,和
时,和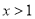 时的符号即可.(ⅱ)由(ⅰ)可知
时的符号即可.(ⅱ)由(ⅰ)可知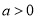 .
.
试题解析:【解析】
(1)①0是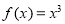 的“? -点”;
的“? -点”;
②0不是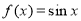 的“? -点”. 2分
的“? -点”. 2分
(2)当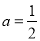 时,
时,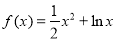 .其定义域为
.其定义域为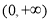 ,
,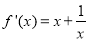 (
(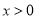 ).
).
(ⅰ)因为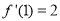 ,
,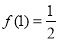 .
.
所以 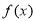 在点
在点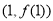 处的切线方程为
处的切线方程为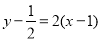 ,
,
即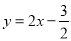 . 4分
. 4分
令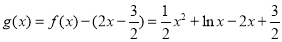 .
.
则 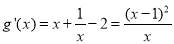 . 5分
. 5分
因为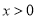 ,
,
所以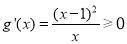 .
.
所以 函数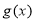 是
是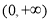 上的增函数. 7分
上的增函数. 7分
所以 当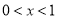 时,
时,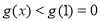 ,即
,即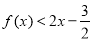 ;
;
当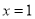 时,
时,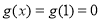 ,即
,即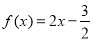 ;
;
当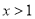 时,
时,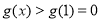 ,即
,即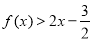 .
.
所以 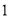 是函数
是函数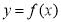 的 “? -点”. 10分
的 “? -点”. 10分
(ⅱ)若函数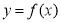 存在“? -点”,则
存在“? -点”,则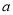 的取值范围是
的取值范围是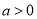 . 14分
. 14分
考点:1新概念问题;2用导数研究函数的性质.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:选择题
已知x,y满足不等式组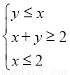 ,则z=2x+y的最大值与最小值的比值为( )
,则z=2x+y的最大值与最小值的比值为( )
A、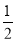 B、2 C、
B、2 C、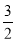 D、
D、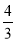
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试理科数学试卷(解析版) 题型:选择题
已知等差数列 的公差为 2,若前 17 项和为
的公差为 2,若前 17 项和为  ,则
,则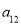 的值为( )
的值为( )
A.-10 B.8 C.4 D.12
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试文科数学试卷(解析版) 题型:选择题
一个函数f(x),如果对任 意一 个三 角形 ,只要它的三边长a,b,c都在f(x)的定 义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“三角保型函数”,给 出下 列函 数:① f(x)=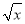 ,②
,②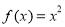 ;③f(x)=2x ;④f(x)=?lg x ,其中是“三角保型函数”的是( )
;③f(x)=2x ;④f(x)=?lg x ,其中是“三角保型函数”的是( )
A.①② B.①③ C.②③④ D.③④
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试文科数学试卷(解析版) 题型:选择题
已知某几何体的正视图与侧视图都是边长为 1 的正方形,且体积为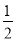 ,视图可以是,则该几何体的俯视图可以是( )
,视图可以是,则该几何体的俯视图可以是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届北京市海淀区高三上学期期中练习文科数学试卷(解析版) 题型:选择题
设等差数列 的前
的前 项和为
项和为 .在同一个坐标系中,
.在同一个坐标系中,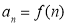 及
及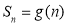 的部分图象如图所示,则( )
的部分图象如图所示,则( )

(A)当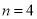 时,
时, 取得最大值
取得最大值
(B)当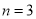 时,
时, 取得最大值
取得最大值
(C)当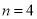 时,
时, 取得最小值
取得最小值
(D)当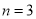 时,
时, 取得最小值
取得最小值
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)全国第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议,2014年3月在北京开幕.期间为了了解国企员工的工资收入状况,从108名相关人员中用分层抽样方法抽取若干人组成调研小组,有关数据见下表:(单位:人)
| 相关人数 | 抽取人数 |
一般职工 | 63 |
|
中层 | 27 |
|
高管 | 18 | 2 |
(1)求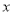 ,
,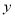 ;
;
(2)若从中层、高管抽取的人员中选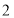 人,求这二人都来自中层的概率.
人,求这二人都来自中层的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com