
分析 (Ⅰ)由椭圆的离心率公式求得a2=4b2,将点代入椭圆方程,即可求得a和b的值,即可求得椭圆方程;
(Ⅱ)设直线方程,代入椭圆方程,利用韦达定理求得|x1-x2|,则△OAB的面积S=$\frac{1}{2}$|m||x1-x2|,利用基本不等式的性质,即可求得△OAB面积的最大值.
解答 解:(Ⅰ)由已知得e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{\sqrt{3}}}{2}$,a2=4b2,
将$(-\sqrt{3},\frac{1}{2})$代入椭圆方程:$\frac{3}{4{b}^{2}}+\frac{1}{4{b}^{2}}=1$,解得a2=4,b2=1,…(2分)
椭圆C的方程是$\frac{{x}^{2}}{4}+{y}^{2}=1$;…(4分)
(Ⅱ)设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2).
将y=kx+m代入椭圆C的方程,可得(1+4k2)x2+8kmx+4m2-16=0,
由△>0,可得m2<4+16k2,①
则有x1+x2=-$\frac{8km}{1+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-16}{1+4{k}^{2}}$.…(6分)
∴|x1-x2|=$\frac{4\sqrt{16{k}^{2}+4-{m}^{2}}}{1+4{k}^{2}}$.…(8分)
由直线y=kx+m与y轴交点的坐标为(0,m),
∴△OAB的面积S=$\frac{1}{2}$|m||x1-x2|
=$\frac{2丨m丨\sqrt{16{k}^{2}+4-{m}^{2}}}{1+4{k}^{2}}$=$\frac{2\sqrt{{m}^{2}(16{k}^{2}+4-{m}^{2})}}{1+4{k}^{2}}$=$2\sqrt{\frac{{4{m^2}}}{{1+4{k^2}}}-\frac{m^4}{{(1+4{k^2}{)^2}}}}$…(10分)
设$\frac{m2}{1+4k2}$=t,由①可知0<t<4,
因此S=2$\sqrt{(4-t)t}$≤2$\sqrt{(\frac{4-t+t}{2})^{2}}$=4,故S≤4,
当且仅当4-t=t,即t=2时取得最大值4.
∴△OAB面积的最大值为4.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,三角形的面积公式,基本不等式的性质,考查计算能力,属于中档题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,正视图和侧视图都是腰长为3的全等的等腰三角形,若该几何体的四个顶点在空间直角坐标系O-xyz的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标为( )
一个几何体的三视图如图所示,正视图和侧视图都是腰长为3的全等的等腰三角形,若该几何体的四个顶点在空间直角坐标系O-xyz的坐标分别是(0,0,0),(2,0,0),(2,2,0),(0,2,0),则第五个顶点的坐标为( )| A. | (1,1,1) | B. | $(1,1,2\sqrt{2})$ | C. | $(1,1,2\sqrt{3})$ | D. | $(2,2,\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源:2017届宁夏高三上月考一数学(理)试卷(解析版) 题型:解答题
已知函数 (
(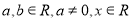 ).
).
(1)若函数 的图象过点
的图象过点 ,函数
,函数 有且只有一个零点,求
有且只有一个零点,求 表达式;
表达式;
(2)在(1)的条件下,当 时,
时, 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届湖北省协作校高三联考一数学(理)试卷(解析版) 题型:选择题
为得到函数 的图象,可将函数
的图象,可将函数 的图象( )
的图象( )
A.向左平移 个单位 B.向左平移
个单位 B.向左平移 个单位
个单位
C.向右平移 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com